Matlab二维绘图

Matlab进阶教程1-二维绘图，包含基本的绘图函数，坐标系的切换，图形窗口，图形标注及特殊图形的绘制（饼图、条形图等）。

Matlab基础教程系列：

Matlab基础0——命令行

Matlab基础1——基础知识

Matlab基础2——向量与多项式

Matlab基础3——元胞与结构体

Matlab基础4——矩阵

Matlab基础5——符号运算

基本绘图函数

plot

最基本的绘图函数。执行plot函数时，若当前已有图形窗口，则将图画在现有图形窗口上，覆盖原有图形；若当前没有图形窗口，则自动创建新的图形窗口。

1	plot(X,Y); % 创建以X为自变量、Y为因变量的二维线图

X和Y必须是同维向量，绘制以X为横坐标、Y为纵坐标的曲线。若：

X是向量，Y是矩阵，则X的维数应与Y的某一维相等，绘制多条颜色不同的曲线，曲线数等于Y的另一维数，X则仍作为横坐标。当Y是方阵时，Matlab会优先处理列，即绘制Y的每一列对X的曲线。
1
2
3
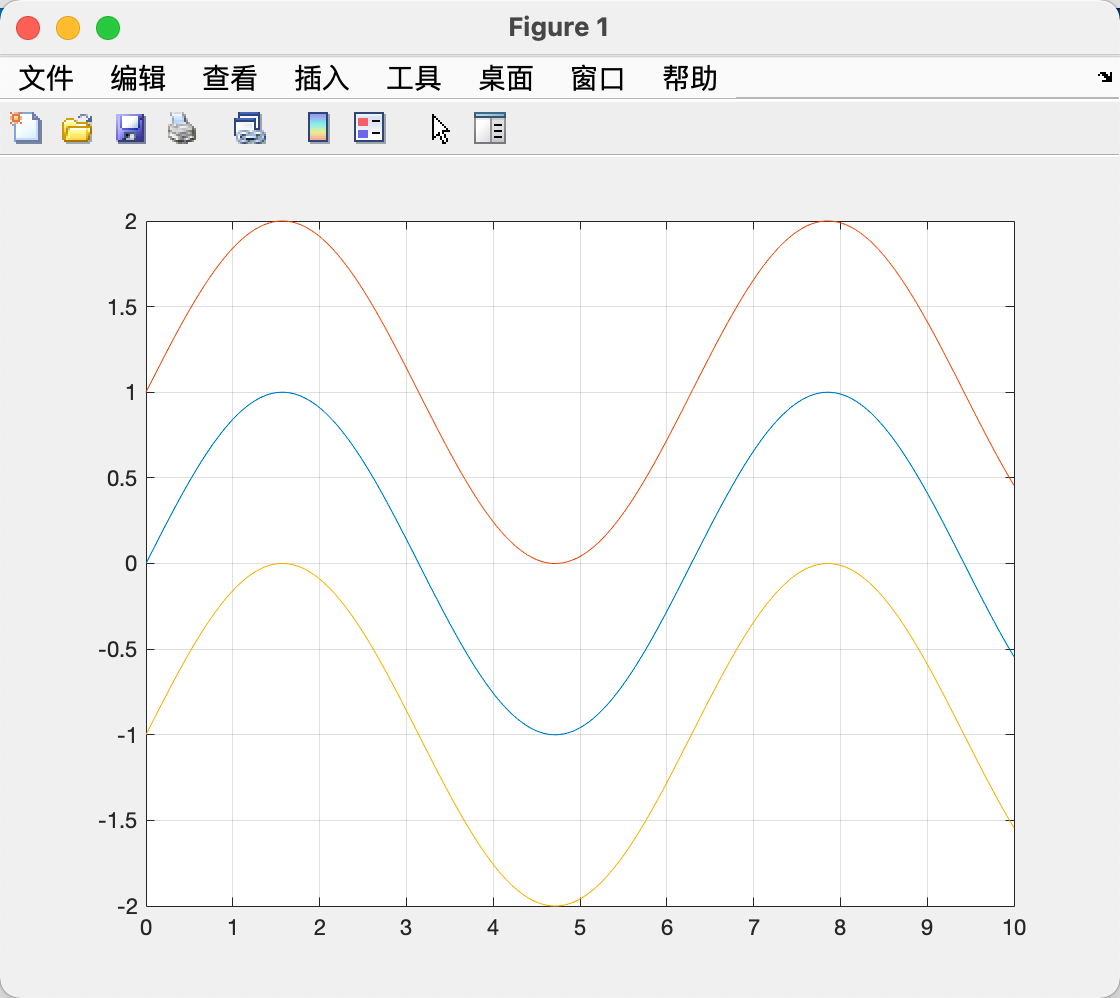
x = 0:0.01:10; % 1*1001
y = [sin(x);sin(x)+1;sin(x)-1]; % 3*1001
plot(x,y); grid on; % 3条曲线
X是矩阵，Y是向量时，规则同上，但**Y会被当作横坐标**
X与Y皆为矩阵时，要求二者必须同维，以X的每一列作为横坐标、以Y对应对列元素作为纵坐标绘制曲线，曲线数等于列数。

1 2	plot(x,y,LineSpec); % 设置线型、标记符号和颜色 plot(x,y,'--or'); % 带有圆形标记的红色虚线

LineSpec是一个字符串，可以包含上述若干要素，基本线型、标记和颜色如下：

线型	说明
`-(default)`	实线
`--`	虚线
`:`	点线
`-.`	点划线

颜色	说明
`w`	白 white
`y`	黄 yellow
`c`	青 cyan
`g`	绿 green
`m`	品 magenta
`r`	红 red
`b`	蓝 blue
`k`	黑 black

标记	说明
`o`	圆圈
`+`	加号
`*`	星号
`.`	点
`x`	叉号
`s`	方形 square
`p`	五角形 pentagonal
`d`	菱形 diamond
`^`	上三角
`v`	下三角
`>`	右三角
`<`	左三角
`h`	六角形 hexagon

ps. 如果仅指定标记而忽略线型，则绘图时不会显示线条，只显示标记。

1 2	plot(x1,y1,...,xn,yn); % 在同一个坐标区域内绘制多张图 plot(x1,y1,LineSpec1,...,xn,yn,LineSpecn);

也可以使用hold on命令，将不同的图画在同一个坐标系里。

1 2	plot(y); % 创建以y中数据为因变量、相应索引为自变量的二维线图 plot(y,LineSpec)

若y是实向量，则x轴刻度范围为 $[1,length(y)]$
若y是实矩阵，则按列绘制曲线，相当于plot(索引矩阵,y)，自变量为索引
若y是复矩阵，则按列绘制曲线，相当于plot(real(y),imag(y))，自变量为实部，因变量为虚部

1
2
3

plot(ax,_);  % 指定坐标范围
plot(_,Name,Value);  % 使用一个或多个(Name,Value)对，单独指定某些属性的值
h = plot(_);  % 用变量h将图形储存，可以通过改变h的属性来实时修改图形

图形线条属性可以通过输出h来查看：

          Color: [0.8500 0.3250 0.0980]  % 颜色
      LineStyle: '-'                     % 线型
      LineWidth: 0.5000                  % 线宽
         Marker: 'none'                  % 符号
     MarkerSize: 6                       % 符号大小
MarkerFaceColor: 'none'                  % 符号填充颜色
          XData: [1×1001 double]         % x轴数据
          YData: [1×1001 double]         % y轴数据
          ZData: [1×0 double]            % z轴数据

修改示例如下：

1
2
3

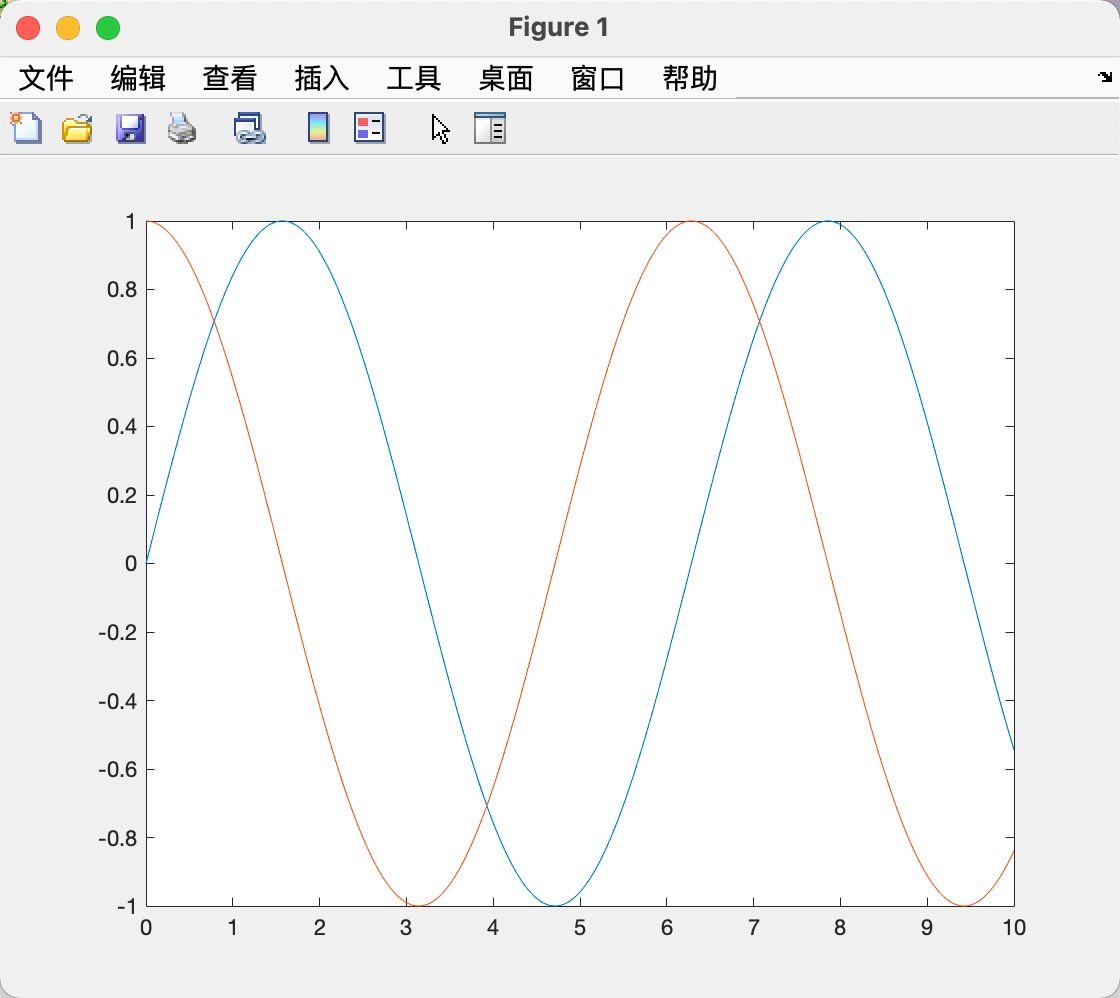
x = 0:0.01:10;
y = [sin(x);cos(x)];
h = plot(x,y);

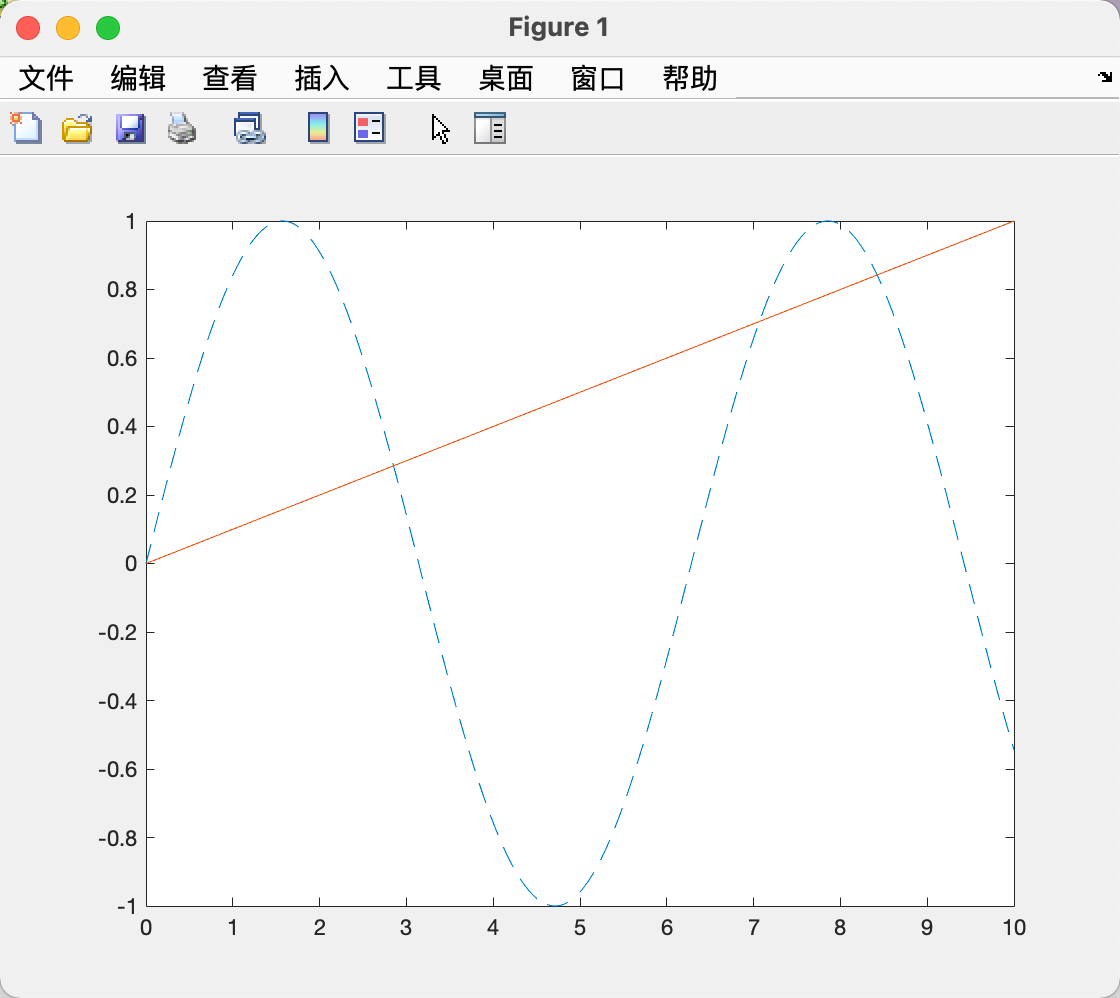
1 2	>> h(2).YData = 0.1*x; % 修改第二条线的y轴数据 >> h(1).LineStyle = '--'; % 修改第一条线的线型

此外，还有一些常用的属性如下

属性	说明	值
`LineJoin`	线条边角样式	`round(default)` `miter` `chamfer`
`MarkerEdgeColor`	标记轮廓颜色	`none(default)` `auto` `颜色`

fplot

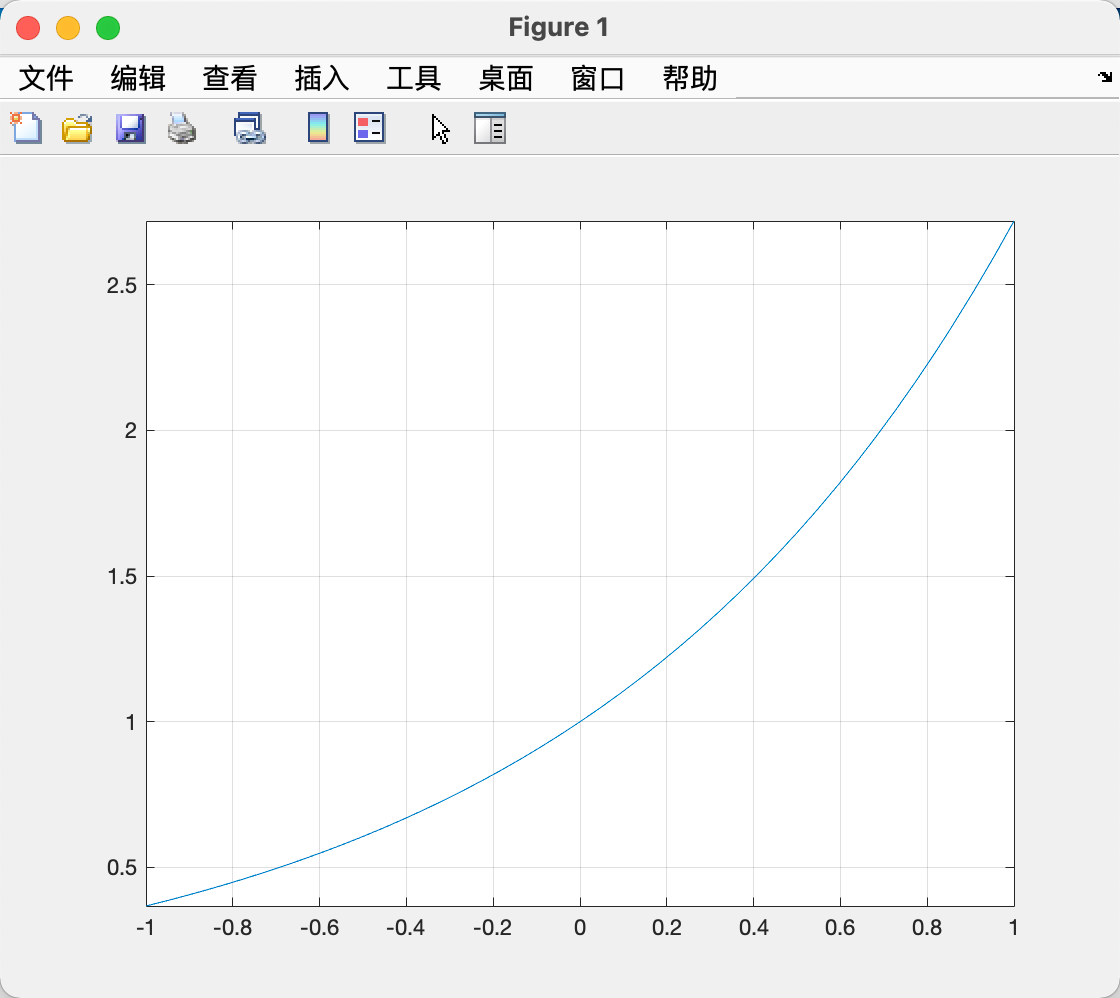
专门用于绘制一元函数的命令。相比于plot()根据指定数据点绘图，fplot()会自适应地选取数据点，即在平滑处选取数据点稀疏、在陡峭处选取数据点密集，使图像更加光滑准确。

1 2	fplot(f); % 在x的默认区间[-5,5]绘制由函数y=f(x)定义的曲线 fplot(f,x_interval); % 在x的指定区间x_interval绘制由函数y=f(x)定义的曲线

f 为m文件函数名或系统自带函数名，x_interval为一个二元向量，包含区间的两个端点。示例如下：

1	fplot(@exp,[-1,1]); grid on;

fplot(funx,funy);
% 在t的默认区间[-5,5]绘制由参数方程x=funx(t),y=funy(t)定义的曲线
fplot(funx,funy,t_interval);
% 在t指定区间t_interval绘制由参数方程x=funx(t),y=funy(t)定义的曲线

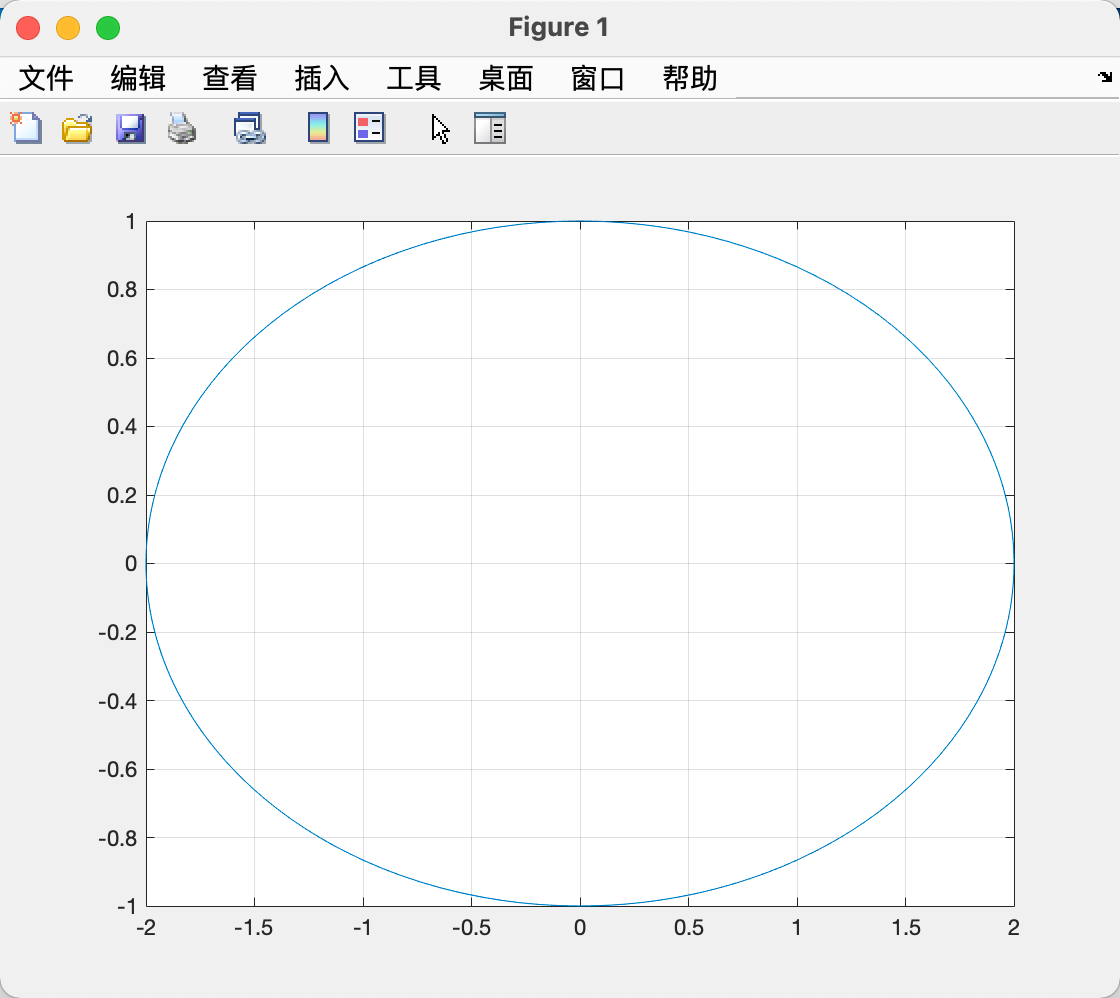
funx和funy为参数方程函数名，t_interval为一个二元向量，包含区间的两个端点。

1
2
3

xt = @(t) 2*cos(t);
yt = @(t) sin(t);
fplot(xt, yt); grid on;

fplot(_,LineSpec);  % 指定线型、标记符号和颜色
fplot(_,Name,Value);  % 指定线条属性
fplot(ax,_);  % 指定坐标范围
fp = fplot(_);  % 返回可修改的图形对象

subplot

用于在同一个图形窗口中分割出多个视图区域。

1	subplot(m,n,p); % 将当前窗口分割成m行n列的区域，用p指定当前位置

对p的编号采用从左至右、从上至下的原则。

1 2	subplot(m,n,p,'replace'); % 将视图替换为空坐标区 subplot('Position',pos); % 在pos指定的自定义位置创建坐标区

pos的格式为[left, bottom, width, height]，即以左下角坐标、宽度和高度定义，若新坐标区与原有坐标区重叠，则原有坐标区会被替换。

不同坐标系下的绘图

上述所有绘图命令均建立在平面直角坐标系中，下面介绍几种其他坐标系的绘图方法。

极坐标系 `polarplot`

与直角坐标系的plot函数几乎一致，只是将x换做theta，将y换做rho

polarplot(theta,rho);  % theta-极角(rad),rho-极半径
polarplot(theta,rho,LineSpec);
polarplot(theta1,rho1,...,thetan,rhon);
polarplot(theta1,rho1,LineSpec1,...,thetan,rhon,LineSpecn);
polarplot(z);  % rho对应复数z的模长，theta对应幅角主值
polarplot(z,LineSpec);
ploarplot(_,Name,Value);
p = polarplot(_);

示例：

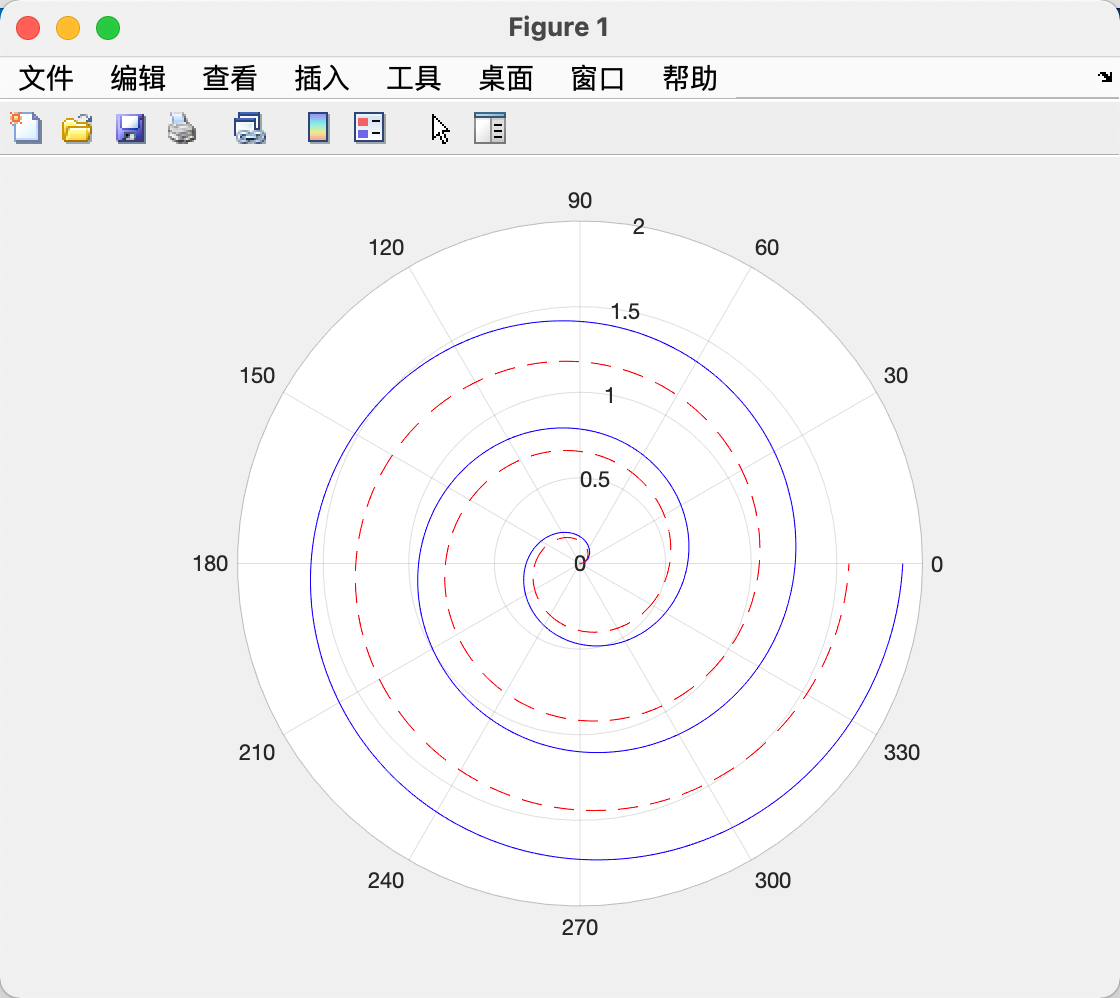
theta = 0:0.01*pi:6*pi;
rho1 = theta/10;
rho2 = theta/12;
polarplot(theta,rho1,'-b',theta,rho2,'--r');

坐标转化：

[theta, rho] = cart2pol(x, y);  % 直角坐标转极坐标
[x, y] = pol2cart(theta, rho);  % 极坐标转直角坐标
R = deg2rad(D);  % 角度转弧度
D = rad2deg(R);  % 弧度转角度

对数坐标系

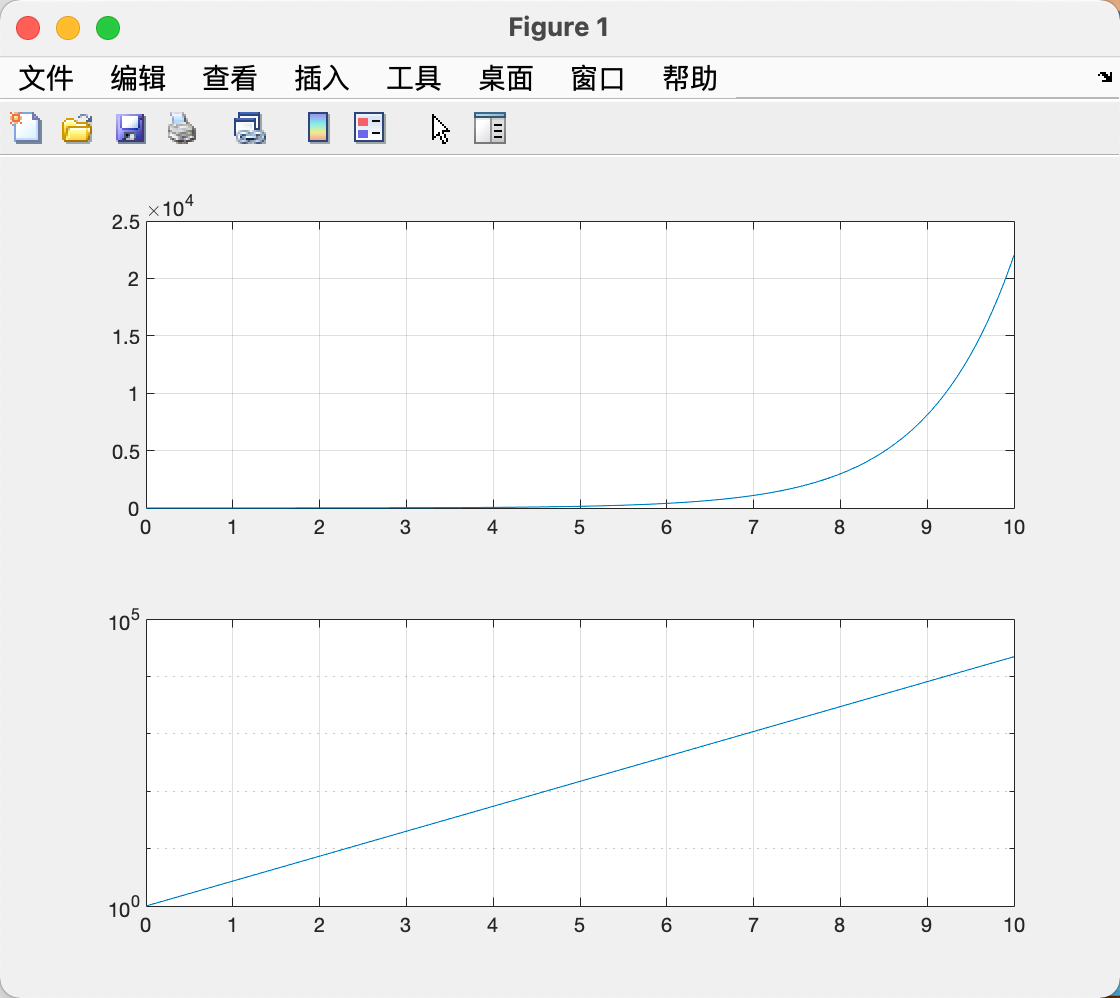
对于某些变化迅速的变量，线性坐标可能无法形象展示其变化过程。若将部分或全部坐标取对数，就可以减缓变量的变化过程。常用的对数坐标系有：

semilogx() - x轴为对数坐标，y轴为线性坐标
semilogy() - y轴为对数坐标，x轴为线性坐标
loglog() - x、y轴均为对数坐标

函数调用规则与plot类似。示例如下：

x = 0:0.01:10;
y = exp(x);
subplot(2,1,1); plot(x,y); grid on;  % 直接绘制
subplot(2,1,2); semilogy(x,y); grid on;  % 对y轴取对数

ps. 对数以10为底

双y轴坐标系

对于同一个坐标系内的两条曲线，若二者的变化范围差距过大，会导致变化范围较小的曲线无法清晰显示。此时，可以使用yyaxis left与yyaxis right命令为坐标系创建两个y轴，并分别绘制。该命令仅起到定位作用，与subplot类似。

示例如下：

x = 0:0.01:10;
y_large = sin(x);
y_small = 0.1*cos(x);
subplot(2,1,1); plot(x,y_large,x,y_small); grid on;
subplot(2,1,2); grid on;
yyaxis left; plot(x,y_large);
yyaxis right;plot(x,y_small);

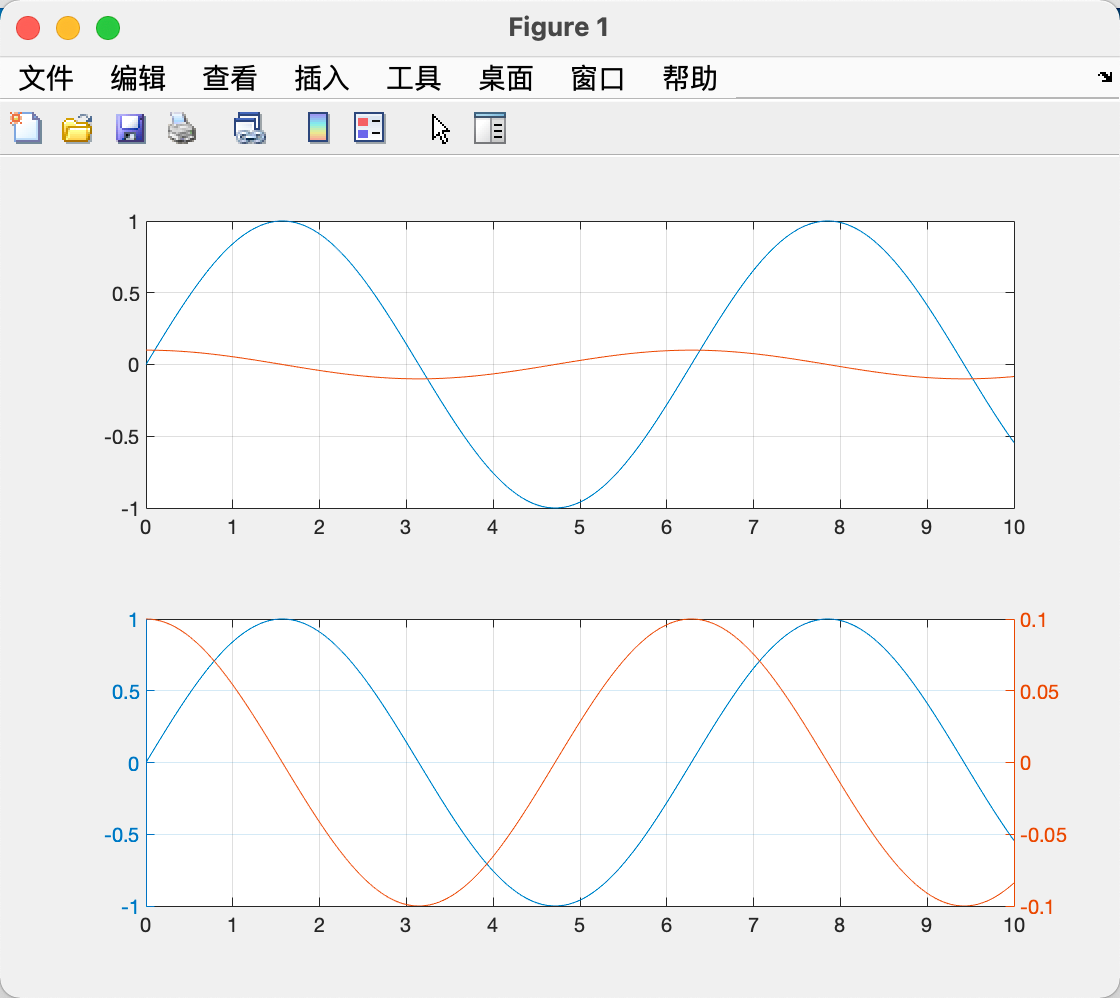
图形窗口

Matlab的图形窗口和命令行窗口是相互独立的，通过图形窗口可以修改和编辑图形界面、实现大量数据计算结果的可视化。

创建

使用figure命令创建图形窗口

figure  % 创建一个图形窗口
figure(Name,Value);  % 使用(Name,Value)对来修改属性，如('Name','图1')
f = figure(_);  % 使用变量f储存窗口对象，可以通过它改变窗口的属性
figure(f);  % 指定当前绘图窗口为f
figure(num);  % 创建一个编号为num的图形窗口

命令	说明
`set(f,[Name1,...],[Value1,...])`	设定图形窗口的属性值
`get(f)`	获取图形窗口的属性值
`close` `close all`	关闭图形窗口
`clf`	清空图形窗口（不会关闭）

图形标注

坐标轴范围

使用axis(limit)指定当前坐标区的范围，limit只能是长度为4、6、8的向量。

1
2
3

axis([Xmin,Xmax,Ymin,Ymax]);  % 2维
axis([Xmin,Xmax,Ymin,Ymax,Zmin,Zmax]);  % 3维
axis([Xmin,Xmax,Ymin,Ymax,Zmin,Zmax,Cmin,Cmax]);  % 4维

图形注释

fill(x,y,'color');  % 用指定颜色填充数据(x,y)构成的多边形
title('string');  % 为图形添加标题
xlabel('string');  % 为x轴添加标注
ylabel('string');
zlabel('string');
text(x,y,'string');  % 在指定位置添加字符串

可以配合num2str(num)函数，为图像添加与数值有关的标注，字符串之间使用[]衔接。

x = 0:0.01:10;
k = rand(1,1);
y = sin(x) * k;
plot(x, y);
title(['k=', num2str(k)]);  % 标题显示随机数k的取值

图例

legend(label1,...,labeln);  % 按照曲线顺序设置图例
legend(_,'Location',lcn);  % 指定图例的位置
% 'north'|'south'|'east'|'west'|'northeast'|...
legend(_,'Orientation',ornt);  % 指定图例的显示方式
% 'vertical'(defalut)|'horizontal'

网格线

1
2
3

grid on;  % 为当前坐标区添加主网格线
grid;  % 切换主网格线可见性
grid minor;  % 切换次网格线可见性

绘制特殊图形

条形图`bar`

1 2	bar(y); % 创建一个条形图，y中的每个元素对应一个条形。 bar([1,2,3,4,5]);

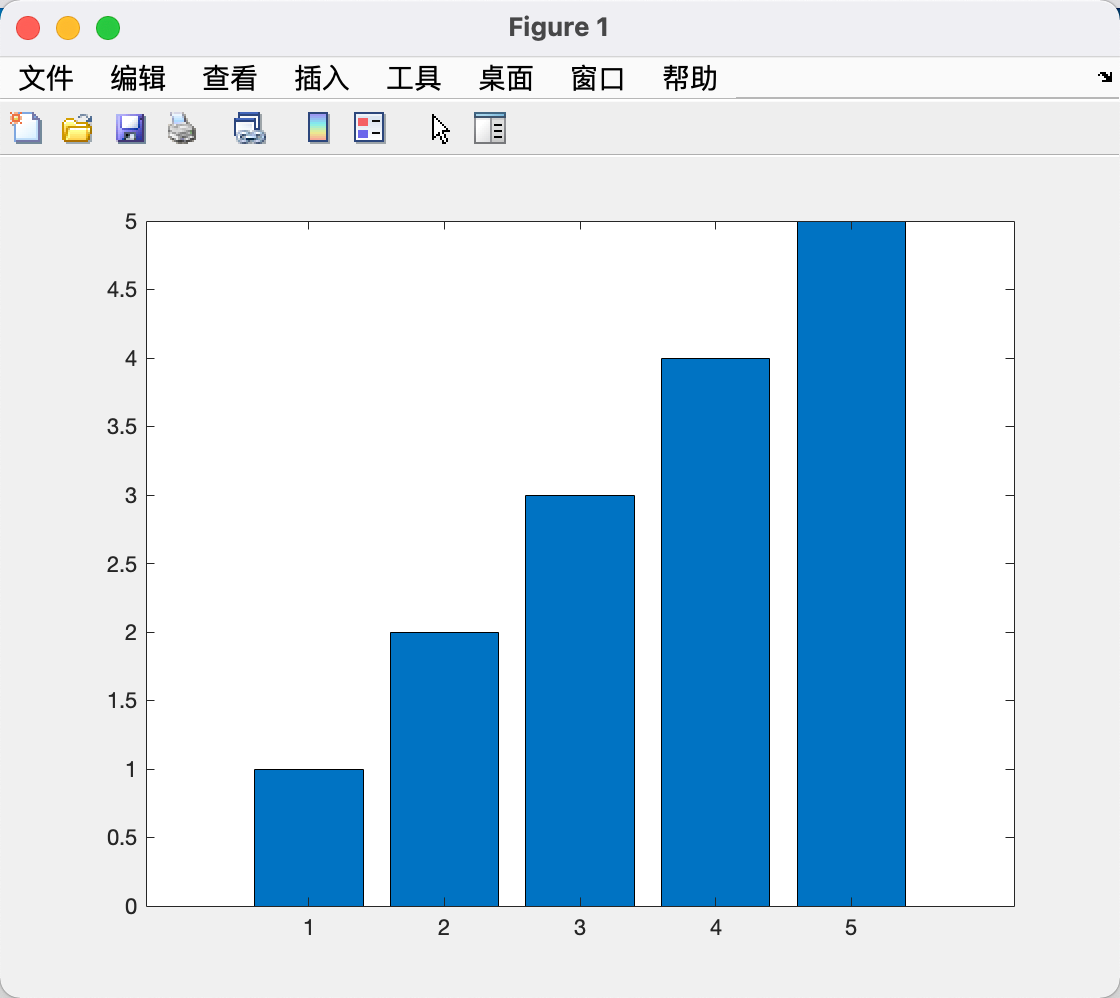
当y是 $m\times n$ 的矩阵时，创建 $m$ 组，每组包含 $n$ 个条形：

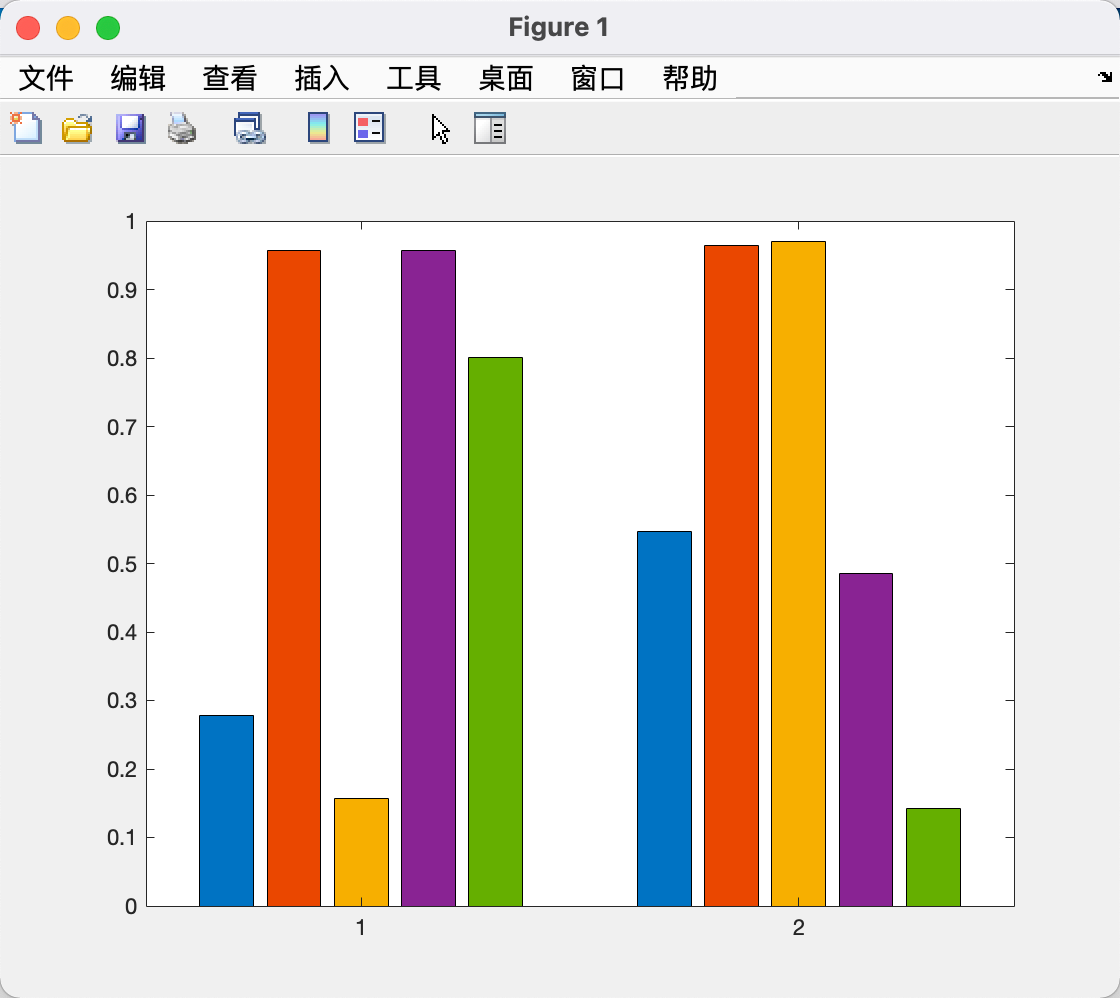
1	bar(rand(2,5));

bar(x,y);  % 在横坐标x指定的位置绘制y，要求x为严格单调递增的向量
bar(_,width);  % 设置条形的相对宽度
bar(_,style);  % 设置条形组的样式 
% 'grouped'(defalut)|'stacked'|'hist'|'histc'
bar(_,color);  % 设置条形的颜色
b = bar(_);  % 保存对象，可以修改其属性值

此外，还有其他形式的条形图，调用格式类似：

函数	说明
`barh()`	水平条形图
`bar3()`	竖直三维条形图
`bar3h()`	水平三维条形图

区域图`area`

area(x);  % 与plot(x)一致，但会将曲线下方区域填充颜色
area(x,y);  % 与plot(x,y)一致，但会将曲线下方区域填充颜色
area(x,Y);  % 矩阵Y按列对向量x绘图，图像依次累加
area(_,basevalue);  % 指定区域填充的基值，默认为0
ar = area(_);  % 保存对象，可以修改其属性值

x = 0:0.5:5;
Y = [ones(size(x))
     rand(size(x))+1
     rand(size(x))+1
     rand(size(x))+1];
area(x,Y',-1);  % 矩阵Y的行数须与向量x一致，指定基值为-1

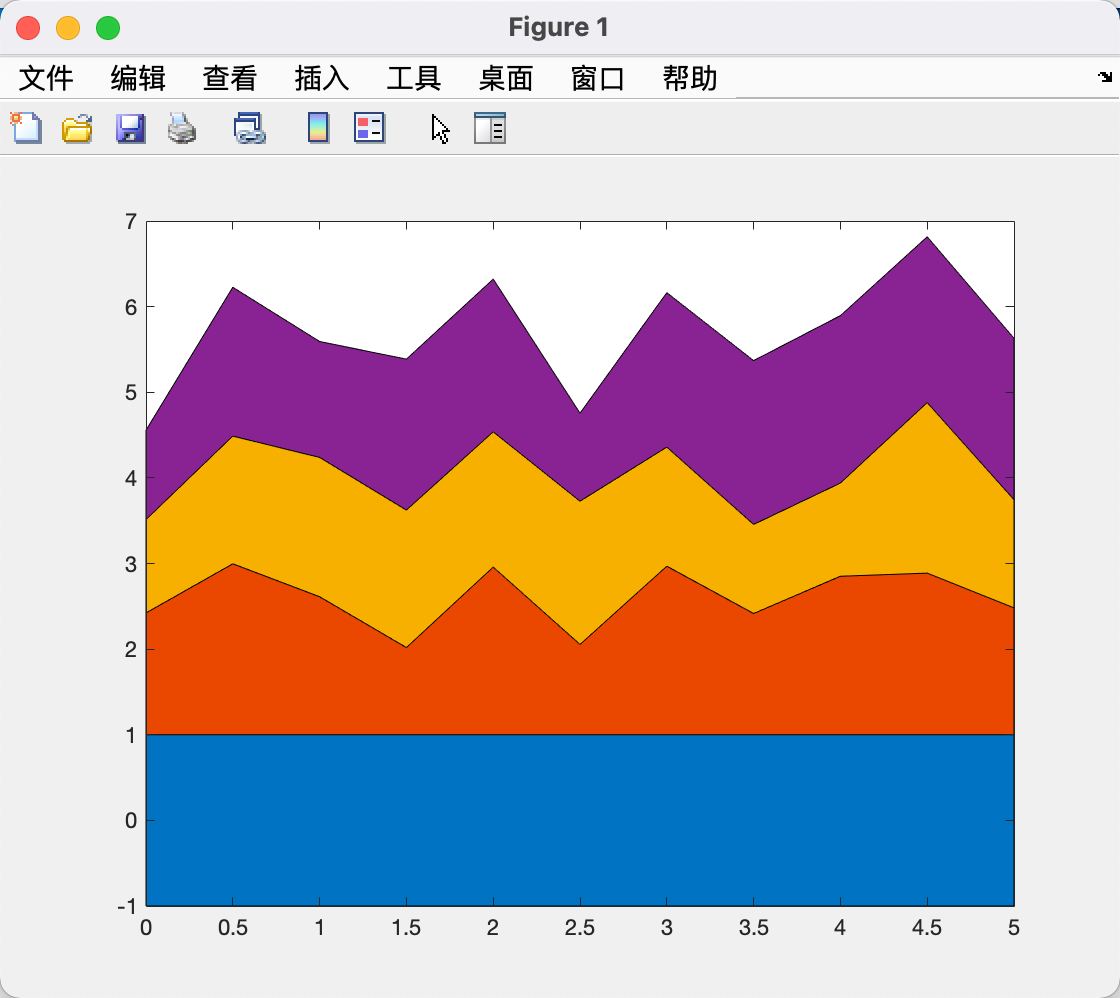
饼图`pie`

pie(x);  % 使用x中的数据绘制饼图
pie(x,explode);  % 将扇区从饼图偏移一定位置
% explode与向量x长度相同，其中的值分别对应偏移大小
pie(x,labels);  % 指定扇区的文本标签，标签数必须等于向量x的长度，采用元胞表示
pie(x,explode,labels);

x = [1, 3, 1, 5];
explode = [0, 0.1, 0.2, 0.3];
labels = {'无偏移', '偏移0.1', '偏移0.2', '偏移0.3'};
pie(x, explode, labels);

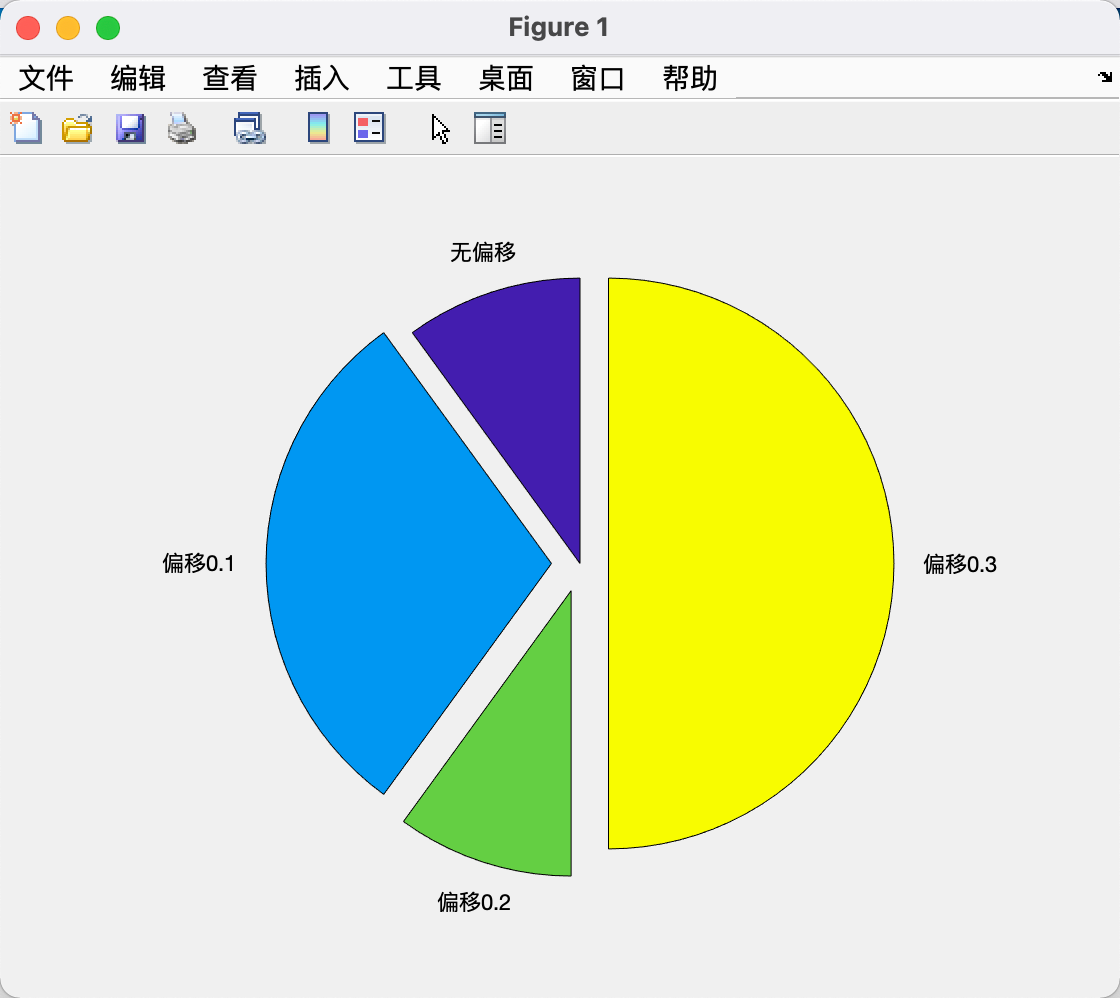
可以用pie3绘制三维饼图。

直方图`histogram`与`polarhistogram`

通过help指令查询详细信息。

1 2	x = randn(10000, 1); histogram(x);

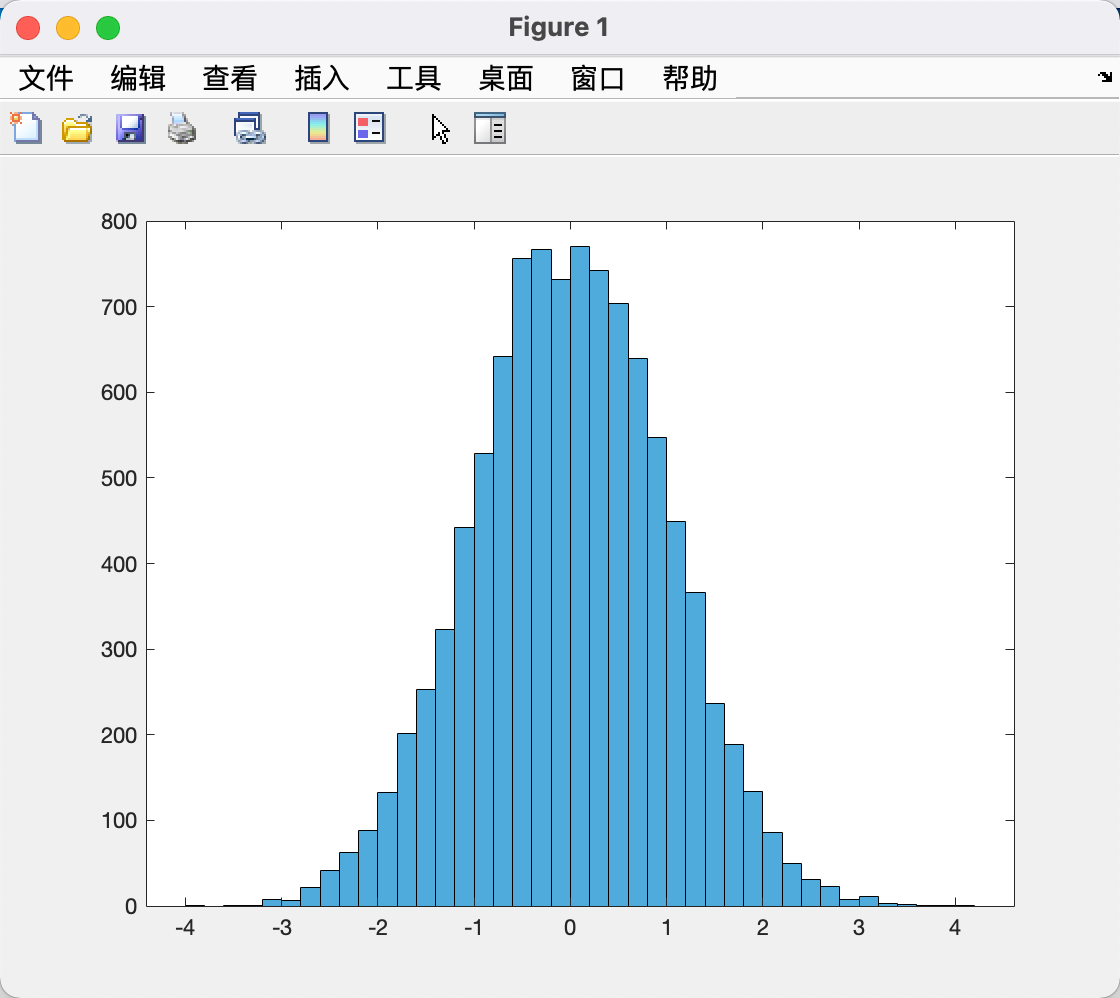
1 2	theta = [0.1 1.1 5.4 3.4 2.3 4.5 3.2 3.4 5.6 2.3 2.1 3.5 0.6 6.1]; polarhistogram(theta,6);

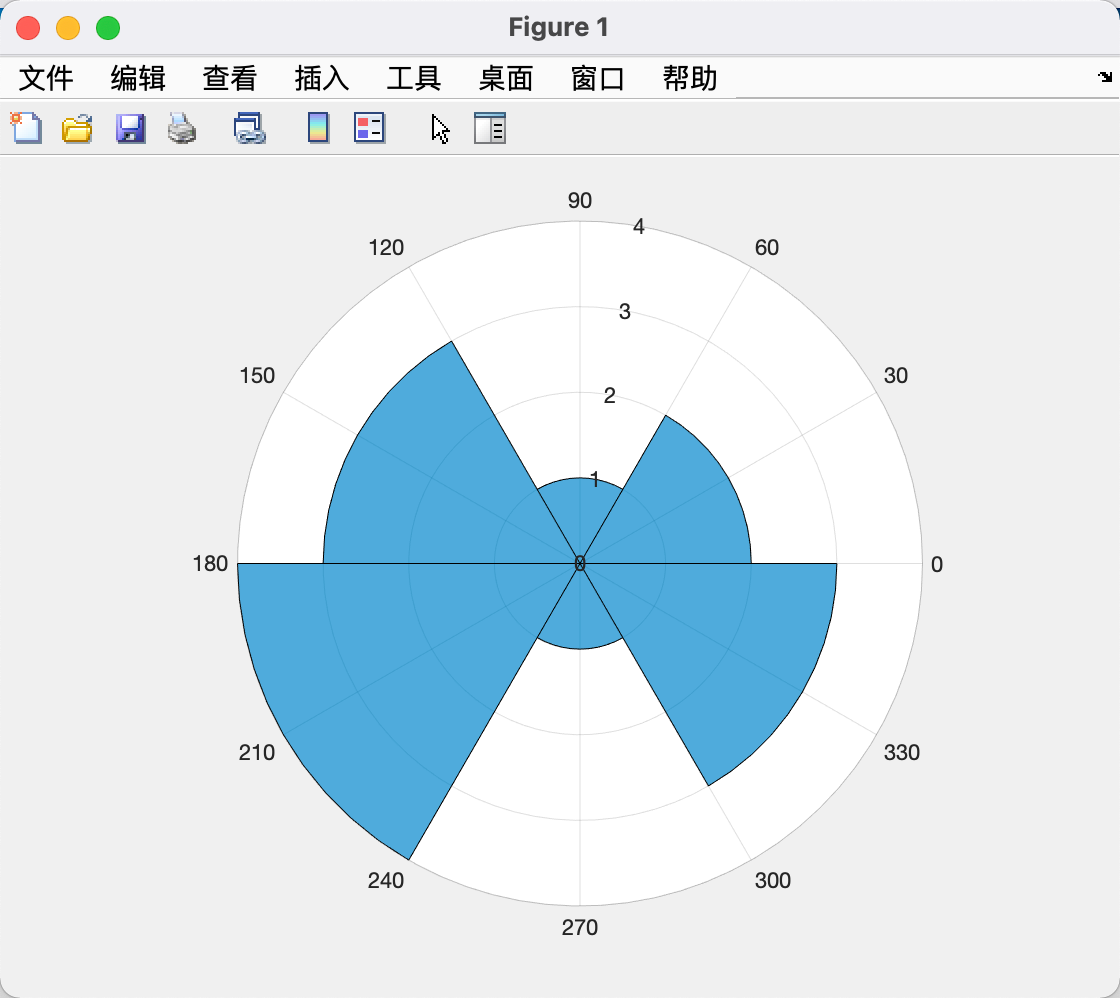
含误差的线图`errorbar`

errorbar(y,err);  % 创建y中数据的线图，并在每个数据点绘制一个垂直误差条
% err和y长度相同，对应了每个数据点的误差大小
errorbar(x,y,err);  % 横坐标x
errorbar(x,y,neg,pos);  % neg确定数据点向下误差，pos确定数据点向上误差
errorbar(_,ornt);  % 设置误差条的方向 'vertical'(default)|'horizontal'|'both'
e = errorbar(_);

x = 1:10;
y = x;
err = [0.1:0.1:0.5, 0.1:0.1:0.5];
errorbar(x,y,err,'both');

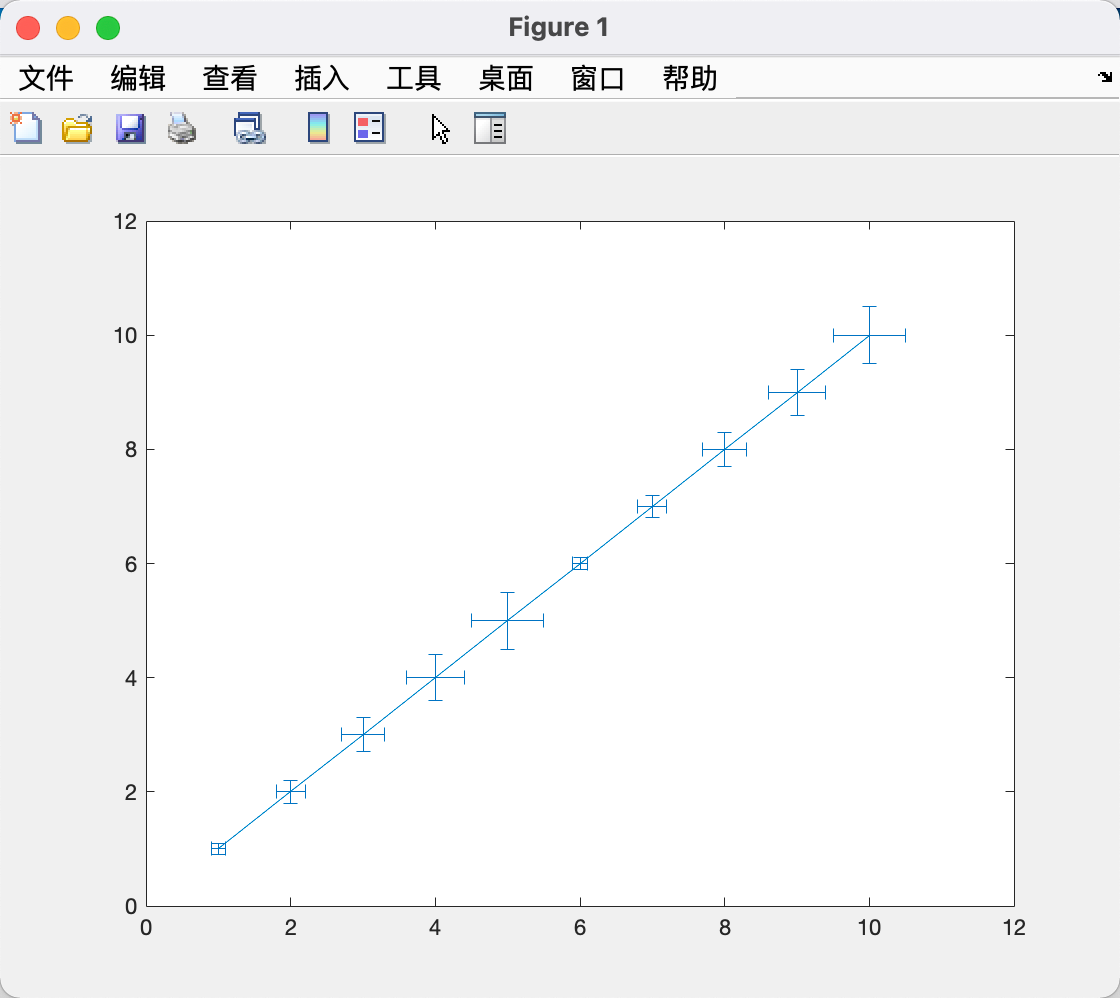
离散图（针状图）`stem`

用法与plot一致。

y = 1:6;
stem(y);
hold on;
stem(y+1,'filled');  % 绘制实心点

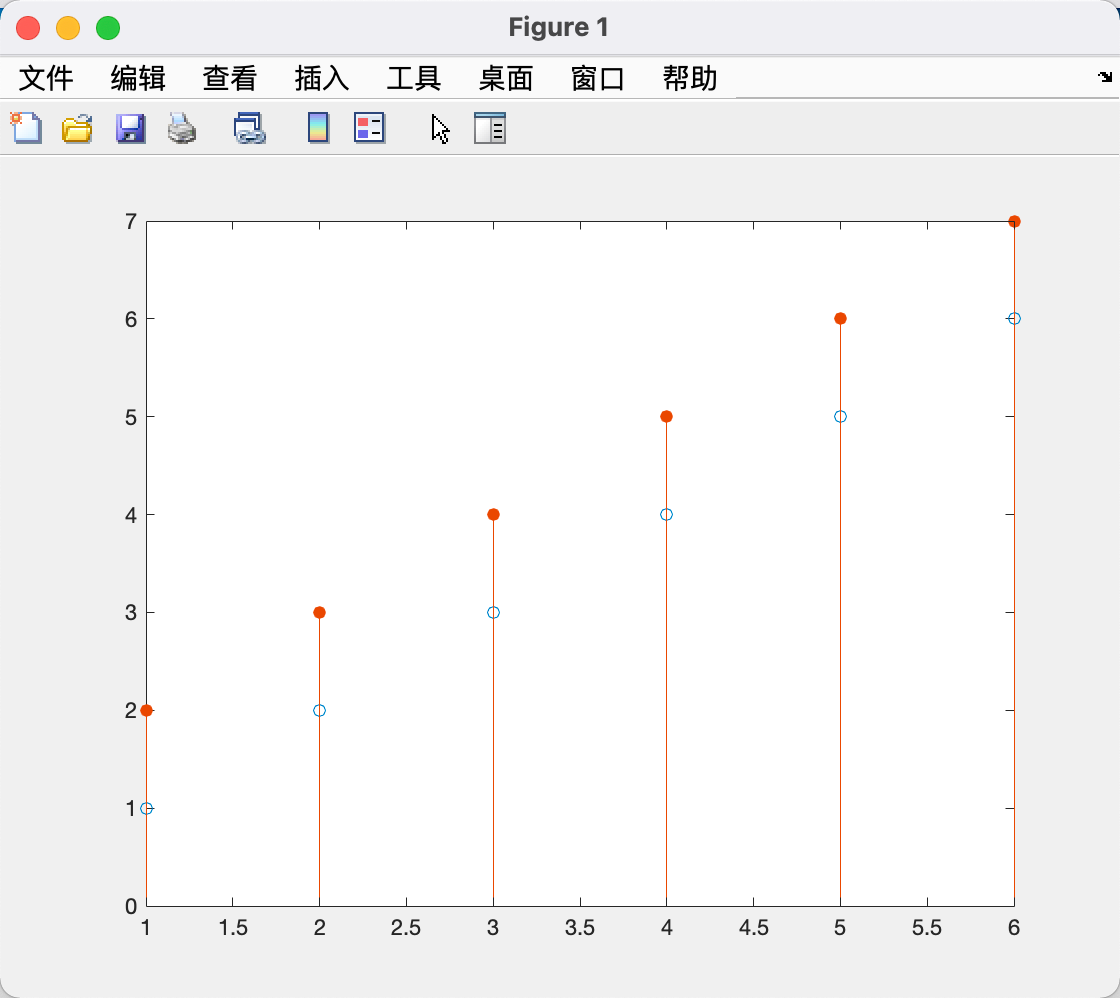
可以用stem3绘制三维针状图

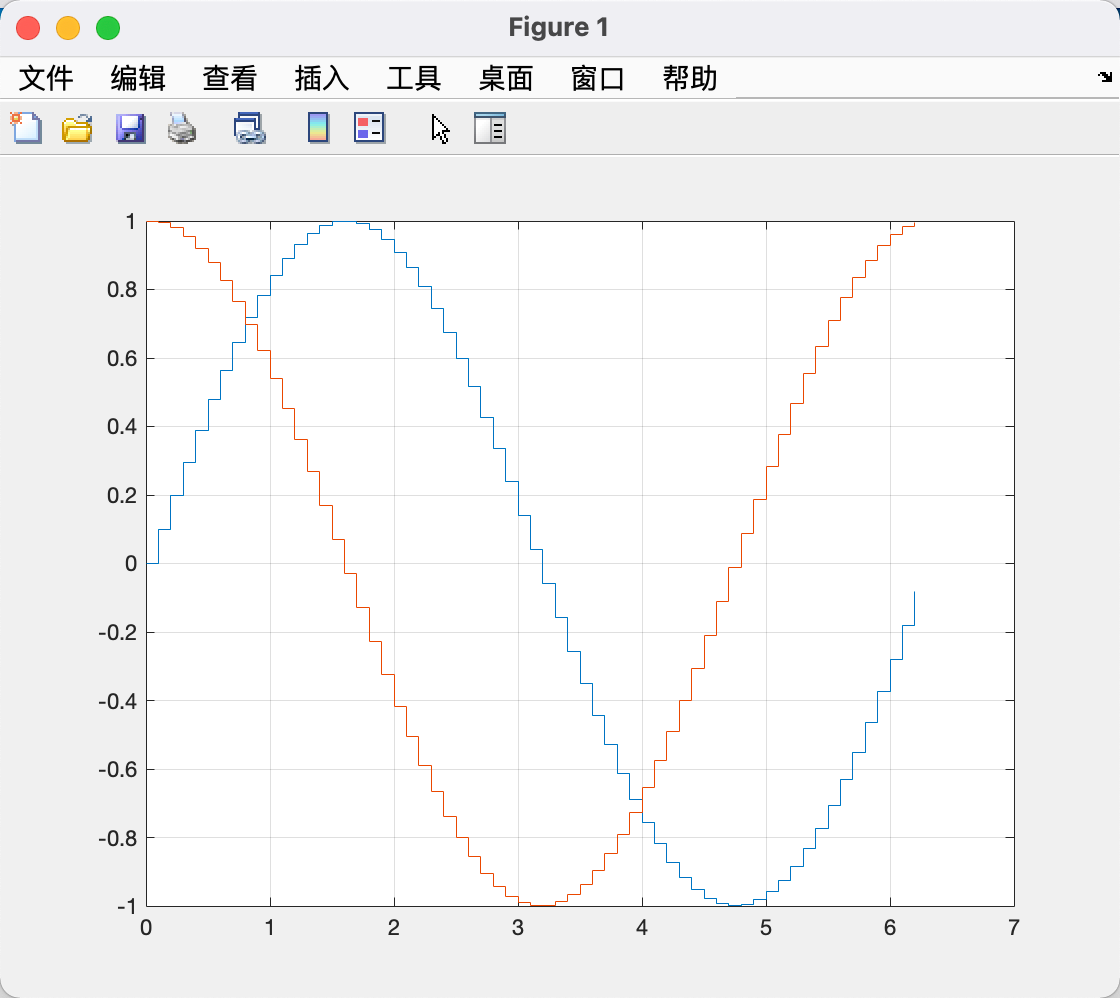
阶梯图`stairs`

用法与plot一致

x = 0:0.1:2*pi;
stairs(x, sin(x));
hold on; grid on;
stairs(x, cos(x));

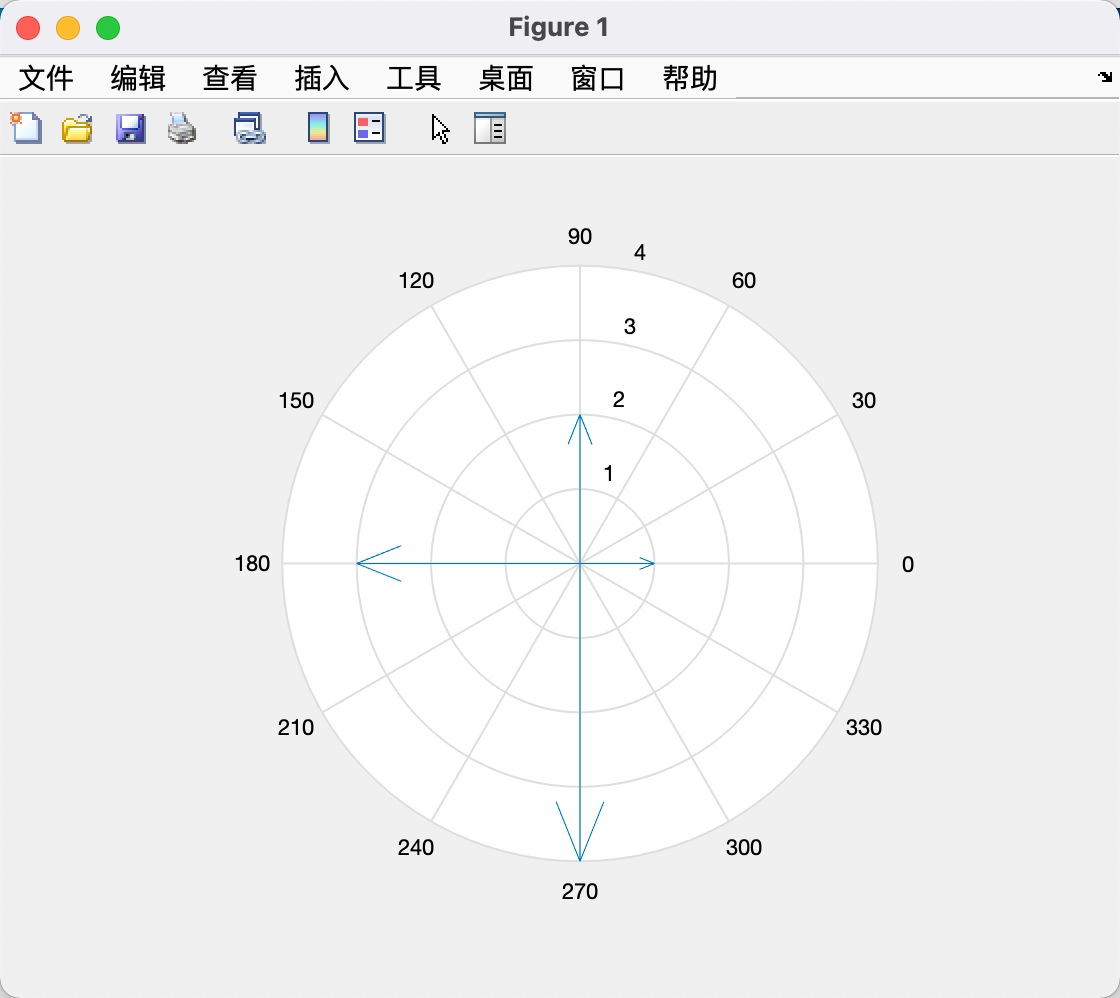
罗盘图`compass`

用箭头显示坐标为 $(u,v)$ 的向量， $u$ 和 $v$ 长度一致，箭头起点位于原点。

1 2	compass(u,v); compass(z); % 相当于compass(real(z), imag(z));

与其他画图函数类似，可以指定线型、标记符号和颜色，可以用对象保存图像。

1
2
3

u = [1, 0, -3, 0];
v = [0, 2, 0, -4];
compass(u,v);

箭头图`quiver`

1 2	quiver(x,y,u,v); % 在(x,y)位置绘制由(u,v)确定的向量 quiver(u,v); % 相当于quiver(1:n,1:m,u,v),其中u,v为m*n的矩阵

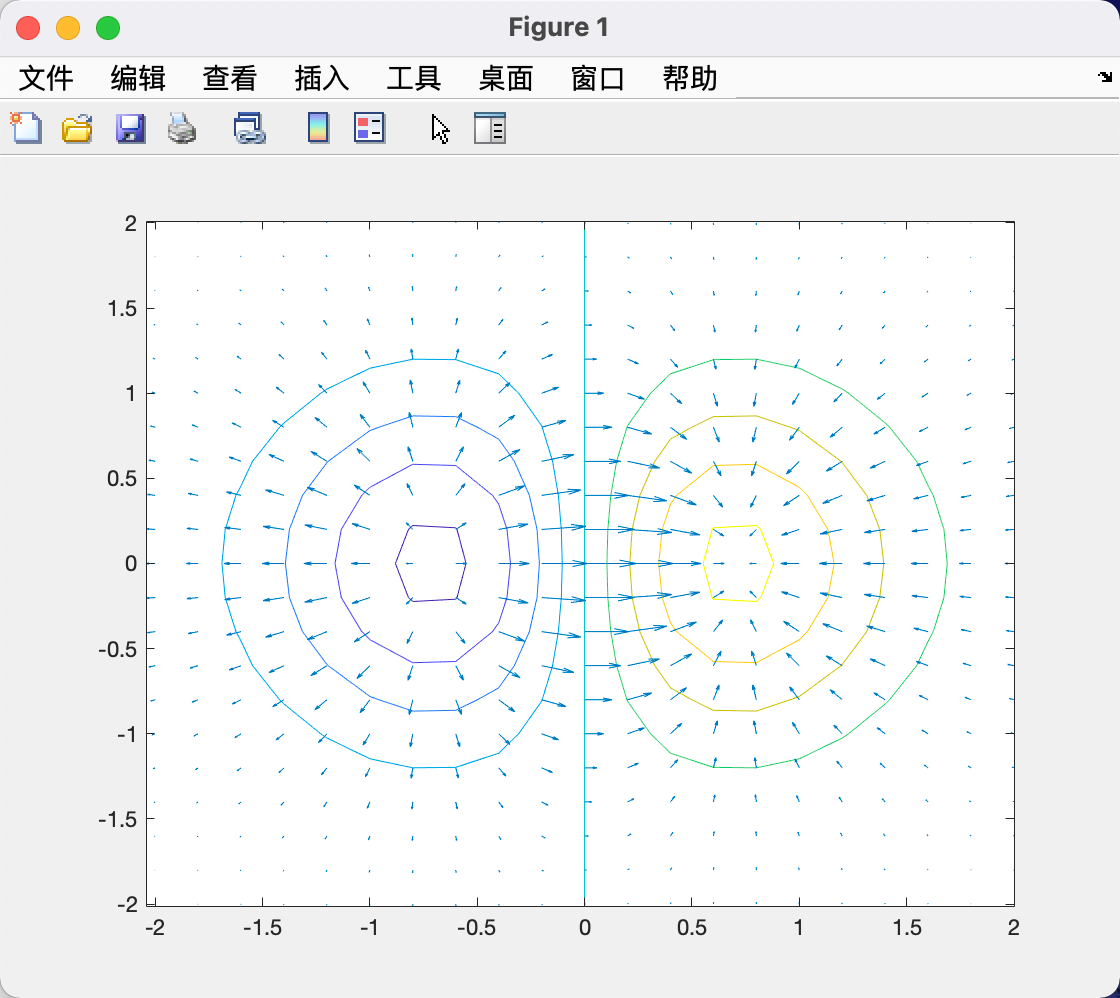
[x, y] = meshgrid(-2:.2:2);  % 返回网格坐标
z = x.*exp(-x.^2 - y.^2);
[dx, dy] = gradient(z, .2, .2);  % 返回梯度

contour(x, y, z);  % 绘制等高线
hold on;
quiver(x, y, dx, dy);

Matlab二维绘图

基本绘图函数

plot

fplot

subplot

不同坐标系下的绘图

极坐标系 polarplot

对数坐标系

双y轴坐标系

图形窗口

创建

相关命令

图形标注

坐标轴范围

图形注释

图例

网格线

绘制特殊图形

条形图bar

区域图area

饼图pie

直方图histogram与polarhistogram

含误差的线图errorbar

离散图（针状图）stem

阶梯图stairs

罗盘图compass

箭头图quiver