菜鸟题解 ZOJ-1239 Hanoi Tower Troubles Again!

原题直达

https://vjudge.net/contest/582185#problem/H

题干

原题面
参考翻译

People stopped moving discs from peg to peg after they know the number of steps needed to complete the entire task. But on the other hand, they didn't not stopped thinking about similar puzzles with the Hanoi Tower. Mr.S invented a little game on it. The game consists of N pegs and a LOT of balls. The balls are numbered 1,2,3... The balls look ordinary, but they are actually magic. If the sum of the numbers on two balls is NOT a square number, they will push each other with a great force when they're too closed, so they can NEVER be put together touching each other.

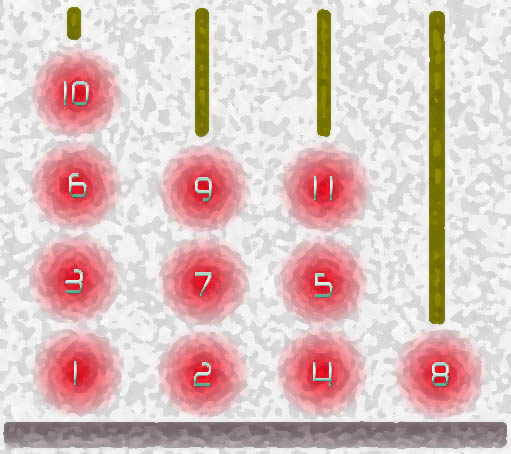
The player should place one ball on the top of a peg at a time. He should first try ball 1, then ball 2, then ball 3... If he fails to do so, the game ends. Help the player to place as many balls as possible. You may take a look at the picture above, since it shows us a best result for 4 pegs.

Input

The first line of the input contains a single integer T, indicating the number of test cases. (1<=T<=50) Each test case contains a single integer N(1<=N<=50), indicating the number of pegs available.

Output

For each test case in the input print a line containing an integer indicating the maximal number of balls that can be placed. Print -1 if an infinite number of balls can be placed.

当人们知道完成整个任务需要走多少步后，他们就不再移动圆盘了。但另一方面，他们并没有停止思考与河内塔类似的谜题。s先生在上面发明了一个小游戏。游戏由N个球钉和许多球组成。球的编号是1,2,3…这些球看起来很普通，但实际上是有魔力的。如果两个球上的数字之和不是平方数，当它们靠得太近时，它们会用很大的力相互推动，所以它们永远不能放在一起碰在一起。

球员每次应该把一个球放在球钉的顶端。他应该先试1号球，然后是2号球，然后是3号球……如果他没有这样做，游戏就结束了。帮助玩家放置尽可能多的球。你可以看看上面的图片，因为它向我们展示了4个挂钩的最佳结果。

Input

输入的第一行包含一个整数T，表示测试用例的数量。(1<=T<=50)每个测试用例包含一个整数N(1<=N<=50)，表示可用的挂钩数量。

Output

对于输入中的每个测试用例，打印一行包含一个整数，表示可以放置的球的最大数量。如果可以放置无限个球，则输出-1。

测试案例

Input

1
2
3

2
4
25

Output

1
2

11
337

题意与思路

题目要求给定 N 根柱子，从编号 1 开始，往每个柱子上串球，要求同一根柱子的 上下相邻两个数字之和是完全平方数。

对于本题，不妨换个思路——在从编号 1 开始串球的过程中，当球放不下的时候，新增一个柱子。

手推几个，就能发现规律：

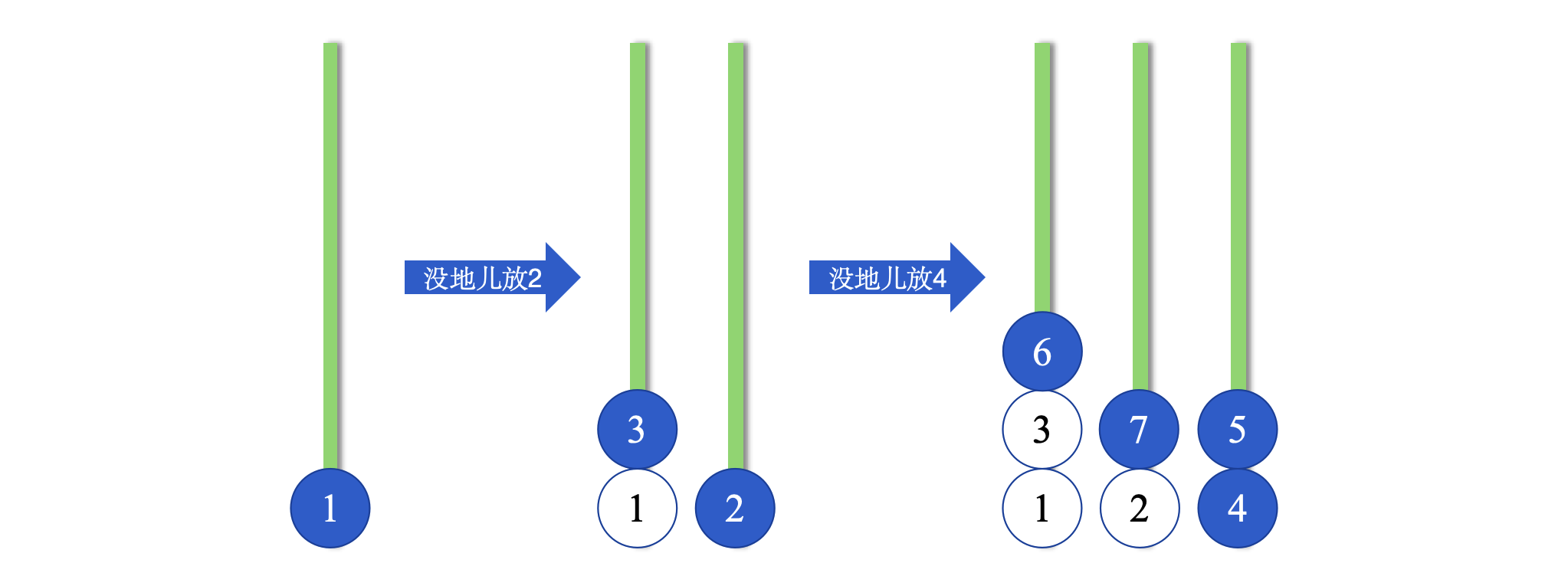
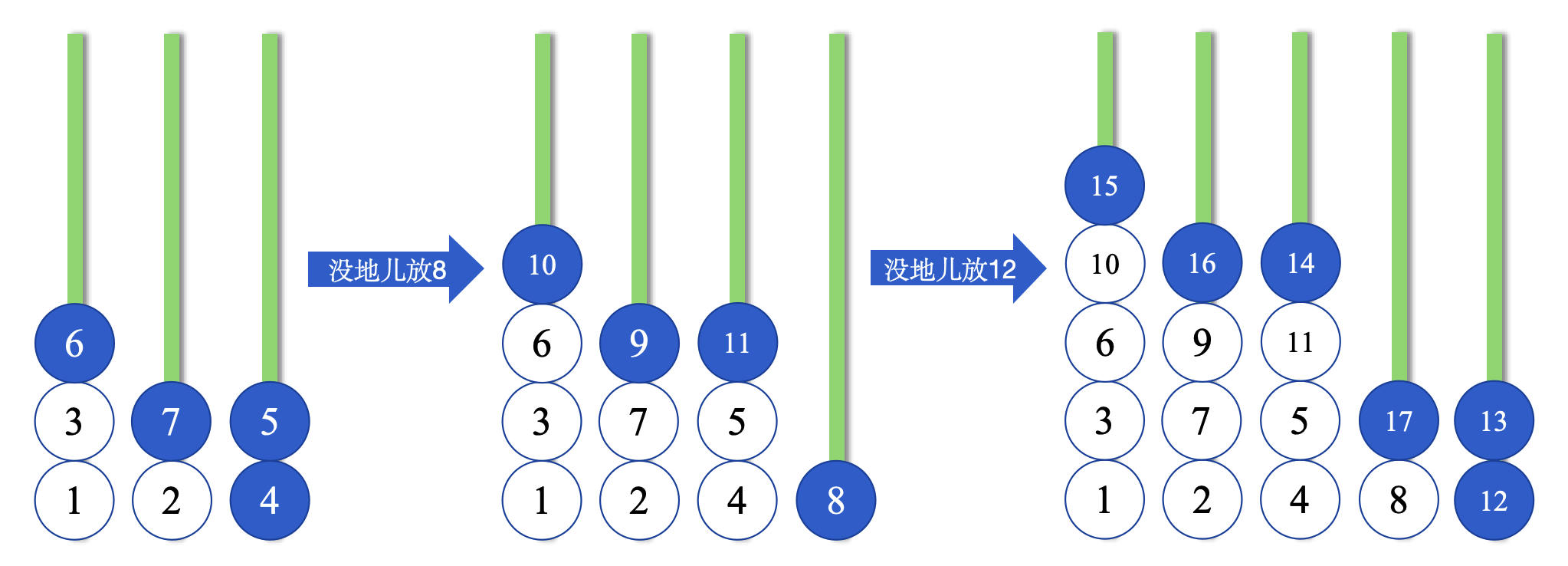
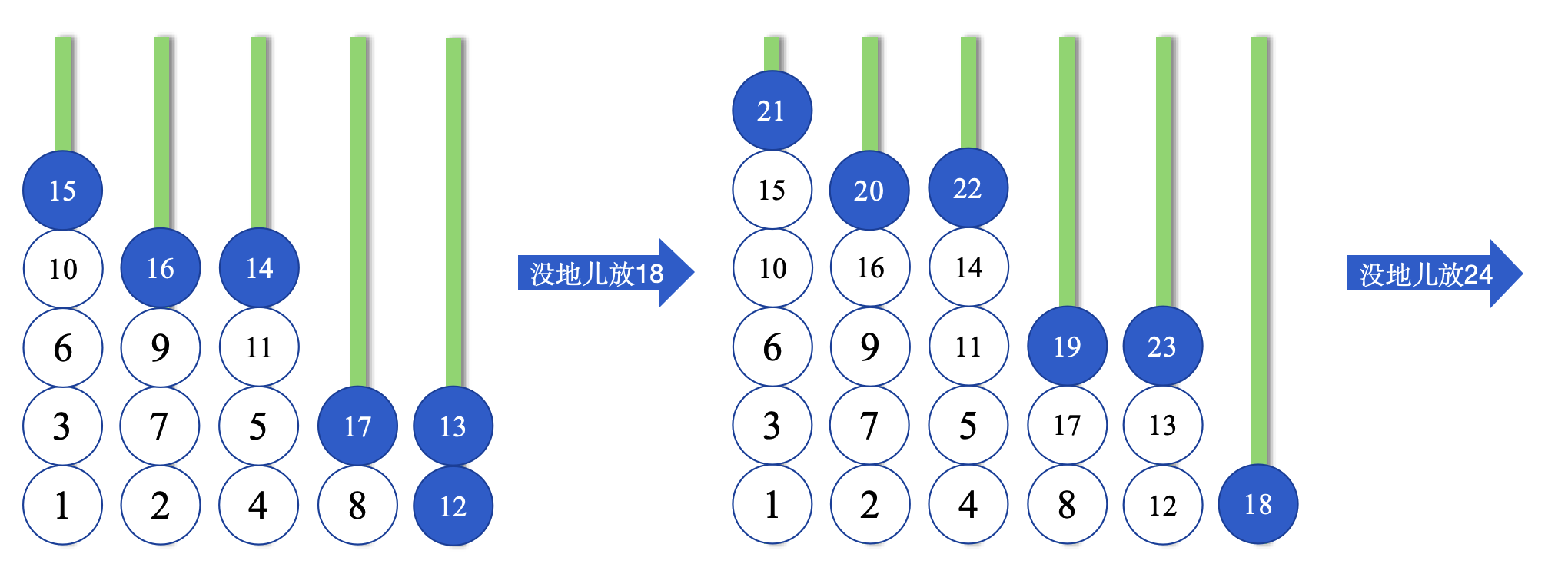
可以看出，每当 N 增加的时候，可以容纳球的个数依次为 +2 +4 +4 +6 +6 +8 +8 ...

表示为代码：

int record[maxn] = {0, 1, 3};  // 初始化N=0, 1, 2时候的情况
void write_record(){
    int cnt = 4;  // 用于记录增量
    for(int i = 3;i <= 50;i++){
        record[i] = record[i-1] + cnt;
        if(i%2 == 0) cnt += 2;
    }
}

因为有点担心会超时，再加上本题对 N 的范围限制在 50 之内，因此考虑将所有结果储存在数组中，需要时直接调用的方法来处理本题：

int record[maxn] = {0,1,3,7,11,17,23,31,39,49,59,71,83,97,111,127,143,161,179,199,219,241,263,287,311,337,363,391,419,449,479,511,543,577,611,647,683,721,759,799,839,881,923,967,1011,1057,1103,1151,1199,1249,1299};

void write_record(){
    int cnt = 4;
    for(int i = 3;i <= 50;i++){
        record[i] = record[i-1] + cnt;
        if(i%2 == 0) cnt += 2;
    }
    
    // 按数组的形式输出结果，复制到上面的数组定义中
    cout<<"{";
    for(int i = 1;i <= 50;i++)
        cout<<record[i]<<",";
    cout<<"}";
}

题解

#include <iostream>

using namespace std;

const int maxn = 60;

int record[maxn] = {0,1,3,7,11,17,23,31,39,49,59,71,83,97,111,127,143,161,179,199,219,241,263,287,311,337,363,391,419,449,479,511,543,577,611,647,683,721,759,799,839,881,923,967,1011,1057,1103,1151,1199,1249,1299};

void write_record(){
    int cnt = 4;
    for(int i = 3;i <= 50;i++){
        record[i] = record[i-1] + cnt;
        if(i%2 == 0) cnt += 2;
    }
    cout<<"{";
    for(int i = 1;i <= 50;i++)
        cout<<record[i]<<",";
    cout<<"}";
}

int main(){
    int T, n;
    cin>>T;
    while (T--){
        cin>>n;
        cout<<record[n]<<endl;
    }
    
    return 0;
}