菜鸟题解 POJ-1328 Radar Installation

原题直达

https://vjudge.net/contest/582185#problem/D

题干

原题面
参考翻译

Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.

We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Figure A Sample Input of Radar Installations

Input

The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.

The input is terminated by a line containing pair of zeros.

Output

For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. “-1” installation means no solution for that case.

假设滑行是一条无限直线。海岸的一边是陆地，另一边是海洋。每个小岛都是位于海边的一个点。而任何雷达装置，定位在海岸上，只能覆盖d距离，所以一个半径的装置可以覆盖一个岛屿，如果他们之间的距离不超过d。

我们用笛卡尔坐标系，定义滑行是x轴。海洋面在x轴上方，陆地面在x轴下方。给定每个岛屿在海上的位置，给定雷达安装的覆盖距离，你的任务是编写一个程序，找出覆盖所有岛屿的最小雷达安装数量。注意，岛屿的位置由它的x-y坐标表示。

图A 雷达安装输入样例

Input

输入由几个测试用例组成。每种情况的第一行包含两个整数n (1<=n<=1000)和d，其中n为海上岛屿的数量，d为雷达安装的覆盖距离。接下来是n行，每一行包含两个整数，代表每个岛屿的位置坐标。然后用空行分隔大小写。

输入以包含一对零的行结束。

Output

对于每个测试用例输出一行，包含测试用例编号，然后是所需雷达安装的最小数量。“-1”安装意味着这种情况下没有解决方案。

测试案例

Input

Output

1 2	Case 1: 2 Case 2: 1

题意与思路

题意为给你若干个海岛的坐标，你需要在海岸线上布置雷达，雷达的覆盖面是半径为 d 的圆形，要求你给出一种布置雷达的方案，使得雷达总数最小。

首先，我们需要判断布置雷达覆盖所有岛屿的方案是否存在，判断条件为：

1	岛屿距离海岸线的距离 <= 雷达覆盖半径

如果方案存在，接下来我们开始探索具体的方案。

对于某个海岛，以其坐标为圆心、d 为半径画圆，在这一范围内布置雷达可以检测到该海岛。由于雷达只能布置在海岸线上，所以实际上，只有该圆与 x 轴相交的区间上有雷达，才能覆盖到这一海岛。

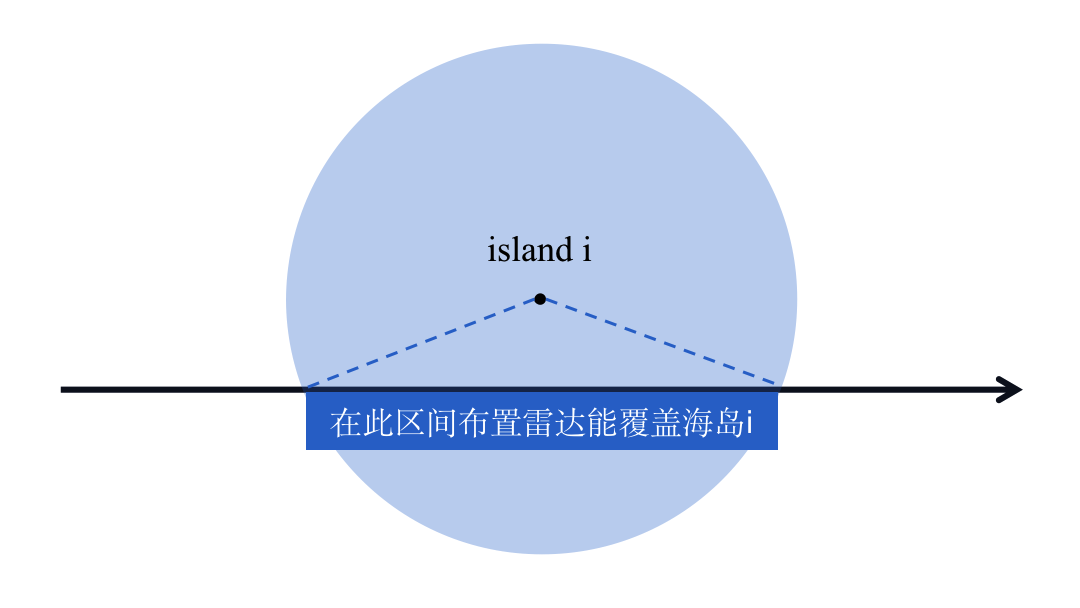
因此，我们可以以海岛为圆心、d 为半径画出若干个圆，尝试遍历这些圆，讨论它们与 x 轴的相交情况以及它们彼此之间的相交情况，就有可能解决这一问题。

按照一般习惯，我们尝试从左到右遍历这些圆，在遍历的过程中布置雷达。雷达可以布置在区间内的任意位置，但是为了使雷达总数最小，我们需要尽可能地让每一个雷达覆盖到更多的海岛。

在从左到右遍历时，我们在当前区间范围内布置一个雷达，并希望它尽可能地照顾到更多右边的海岛，那么这一雷达最佳的位置应该是该区间的右端点。

由此，我们得出了遍历过程中布置雷达的思路：

在第一个岛屿对应区间的右端点布置雷达，记录雷达的位置 raderLoc
考察下一个岛屿，如果：
- 当前处于 raderLoc 位置的雷达可以覆盖到该岛屿，则继续步骤2；
- 当前处于 raderLoc 位置的雷达无法覆盖到该岛屿，则在该岛屿对应区间的右端点布置下一个雷达，并更新雷达的位置 raderLoc；

int rader = 1;  // 记录雷达总数
double raderLoc = 第一个岛屿的区间右端点;

for(int i = 1;i < n;i++){
    if(第i个岛屿能被当前雷达覆盖)
        continue;
    rader ++;  // 新增雷达
    raderLoc = 第i个岛屿的区间右端点;
}

解决了如何布置雷达的问题，还需要解决岛屿的顺序问题。给岛屿排序的思路有很多，例如：

[思路1] 根据岛屿横坐标排序

[思路2] 根据岛屿的区间左端点排序

[思路3] 根据岛屿的区间右端点排序

我们考察下面这种情况：

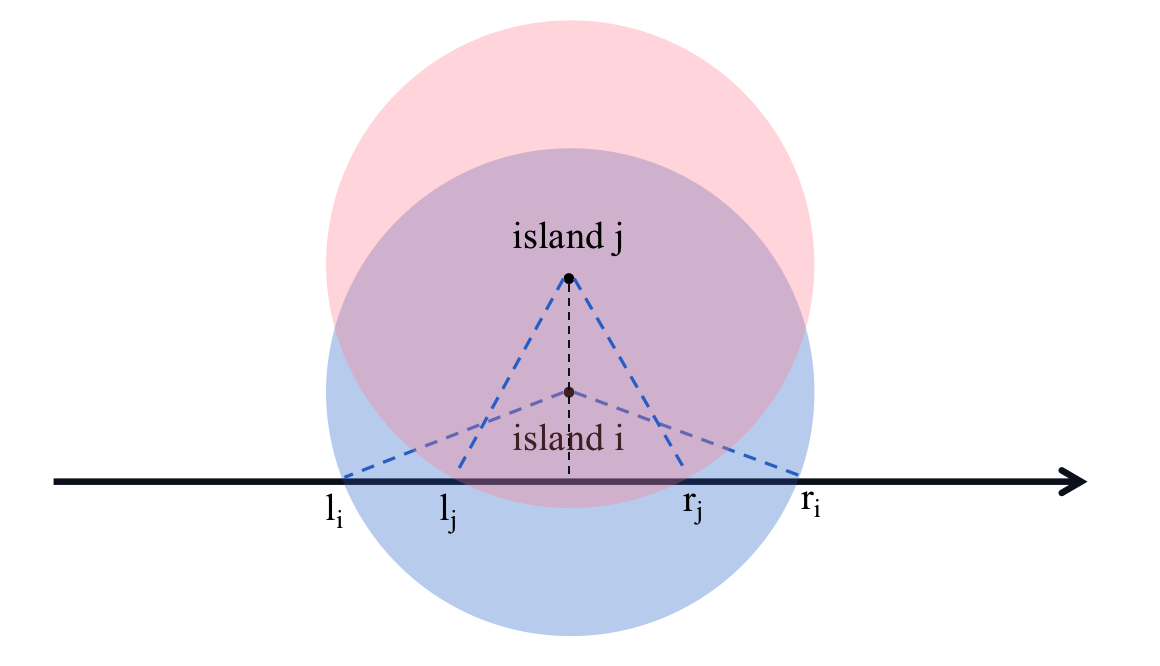
岛屿 i 和岛屿 j 的横坐标相同，对应区间分别为 [li, ri] 和 [lj, rj]，此时：

如果按照区间左端点排序，则 li < lj，遍历时：
- 首先考虑岛屿 i，雷达被布置在 raderLoc = ri
- 接下来考虑岛屿 j，当前雷达位置 raderLoc = ri，无法覆盖到岛屿 j，因此在岛屿 j 的右端点设置下一个雷达 raderLoc = rj
然而，这样就导致岛屿 i 所对应的区间中出现了两个雷达，分别位于 ri 和 rj，产生了浪费，所以这种思路出了问题；

当然，你也可以增加对这种情况的判别，不增设雷达，而是把处于 ri 的雷达挪动到 rj，也是一种可行的思路。
如果按照区间的右端点排序，则 rj < ri，遍历时：
- 首先考虑岛屿 j，雷达被布置在 raderLoc = rj
- 接下来考虑岛屿 i，当前雷达位置 raderLoc = rj，可以覆盖岛屿 i，无需布置新的雷达，与推论相符

因此，我们*采用*[思路3]对所有岛屿进行排序。

我们采用结构体来存储岛屿数据，并定义排序规则 cmp()：

struct node{
    double x;  // 岛屿横坐标
    double y;  // 岛屿纵坐标
    double ro;  // 岛屿对应区间的右端点
    double getRO(){  // 用于计算ro
        return x + sqrt(d * d - y * y);
    }
};

vector<node> vec;  // 用于存储岛屿

bool cmp(node a, node b){
    return a.ro < b.ro;  // 依据区间右端点排序
}

int main(){
    ...
    sort(vec.begin(), vec.end(), cmp);  // 排序
    ...
    return 0;
}

需要特别注意，当有海岛距离海岸线超过 d 即方案不存在时，亦须先等待输入结束，再输出 Case x: -1，而不能检测到该岛屿时直接输出，~~否则会报错，呜呜呜呜呜呜呜~~

需要特别注意2，输入岛屿数据的时候不要用 cin，要用 scanf，因为 cin 比 scanf 慢，会报超时~~呜呜呜呜呜呜呜~~

题解

#include <iostream>
#include <cmath>
#include <vector>
#include <algorithm>
#include <cstdio>

using namespace std;

int n;
double d;

struct node{
    double x;  // 岛屿横坐标
    double y;  // 岛屿纵坐标
    double ro;  // 岛屿对应区间的右端点
    double getRO(){  // 用于计算ro
        return x + sqrt(d * d - y * y);
    }
};

vector<node> vec;  // 用于存储岛屿

bool cmp(node a, node b){
    return a.ro < b.ro;  // 依据区间右端点排序
}

int main(){

    int cnt = 1;  // Case x

    while (scanf("%d %lf", &n, &d) != EOF){
        if(n == 0 && d == 0)
            break;
        vec.clear();  // 清空上一个Case储存的岛屿

        double maxDis = 0;
        for(int i = 0;i < n;i++){
            node t;
            // cin>>t.x>>t.y;
            scanf("%lf %lf", &t.x, &t.y);
            maxDis = max(maxDis, t.y);
            if(maxDis > d) continue;
            t.ro = t.getRO();
            vec.push_back(t);
        }

        cout<<"Case "<<cnt<<": ";
        cnt ++;

        if(maxDis > d){
            cout<<"-1"<<endl;
            continue;
        }

        sort(vec.begin(), vec.end(), cmp);

        int rader = 1;
        double raderLoc = vec[0].ro;

        for(int i = 1;i < n;i++){
            if(d * d >= (vec[i].x - raderLoc) * (vec[i].x - raderLoc) + vec[i].y * vec[i].y)
                continue;
            rader ++;
            raderLoc = vec[i].ro;
        }

        
        cout<<rader<<endl;

    }
    

    return 0;
}