菜鸟题解 HDU-1050 Moving Tables

原题直达

https://vjudge.net/contest/582185#problem/B

题干

原题面
参考翻译

The famous ACM (Advanced Computer Maker) Company has rented a floor of a building whose shape is in the following figure.

The floor has 200 rooms each on the north side and south side along the corridor. Recently the Company made a plan to reform its system. The reform includes moving a lot of tables between rooms. Because the corridor is narrow and all the tables are big, only one table can pass through the corridor. Some plan is needed to make the moving efficient. The manager figured out the following plan: Moving a table from a room to another room can be done within 10 minutes. When moving a table from room i to room j, the part of the corridor between the front of room i and the front of room j is used. So, during each 10 minutes, several moving between two rooms not sharing the same part of the corridor will be done simultaneously. To make it clear the manager illustrated the possible cases and impossible cases of simultaneous moving.

For each room, at most one table will be either moved in or moved out. Now, the manager seeks out a method to minimize the time to move all the tables. Your job is to write a program to solve the manager’s problem.

Input

The input consists of T test cases. The number of test cases T is given in the first line of the input. Each test case begins with a line containing an integer N , 1<=N<=200 , that represents the number of tables to move. Each of the following N lines contains two positive integers s and t, representing that a table is to move from room number s to room number t (each room number appears at most once in the N lines). From the N+3-rd line, the remaining test cases are listed in the same manner as above.

Output

The output should contain the minimum time in minutes to complete the moving, one per line.

著名的ACM(高级计算机制造商)公司租用了一层楼，其形状如下图所示。

这一层沿走廊的南北两侧各有200个房间。最近公司制定了一项制度改革计划。改革包括在房间之间移动许多桌子。因为走廊很窄，所有的桌子都很大，所以只有一张桌子可以通过走廊。为了使搬家更有效率，需要一些计划。经理想出了如下计划:把一张桌子从一个房间搬到另一个房间可以在10分钟内完成。当将桌子从房间i移动到房间j时，使用房间i前面和房间j前面之间的走廊部分。因此，在每10分钟内，在两个房间之间的几个移动将同时进行，而不是共享走廊的同一部分。为了说清楚，经理举例说明了同时搬家的可能情况和不可能情况。

对于每个房间，最多有一张桌子将被搬进或搬出。现在，经理寻找一种方法来最小化移动所有桌子的时间。你的工作是写一个程序来解决经理的问题。

Input

输入由T测试用例组成。测试用例的数量T在输入的第一行给出。每个测试用例都以包含整数N的一行开始，1<=N<=200，表示要移动的桌子的数量。下面的N行中的每一行都包含两个正整数s和t，表示一个表将从房间号s移动到房间号t(每个房间号在N行中最多出现一次)。从第N+3行开始，剩余的测试用例以与上面相同的方式列出。

Output

输出应该包含以分钟为单位完成移动的最小时间，每行一个。

测试案例

Input

Output

1
2
3

10
20
30

题意与思路

题意大概为：

有上图所示两排房间，各200间，中间有一条很窄的走廊
有若干桌子需要从某些房间通过走廊挪动到其他房间
每次挪动无论距离长短均耗时10分钟
走廊很窄，其宽度只能容纳一张桌子
当一次挪动开始时，此后的10分钟内，其他桌子不能出现在它移动的路径中，例如：
- 当有一台桌子开始从 room 10 挪动到 room 1 时，另外一台需要从 room 2 挪动到 room 4 的桌子不能同时开始挪动

首先，可以看出，在这个问题中，room 1 和 room 2 实际上是等效的，因为桌子无论是从前者出发还是从后者出发，需要走的路径完全一致。

因此，我们不妨先将问题简化一下——将两边的房间合并到同一边，将一个个房间视为x轴上的一个个坐标，桌子移动的路线则等效为x轴上的区间。

那么问题就变成了：我们现在有若干个区间，如何在保证区间不相交的前提下，尽可能密集地把它们排列在x轴上的若干层中，使得总层数最小：

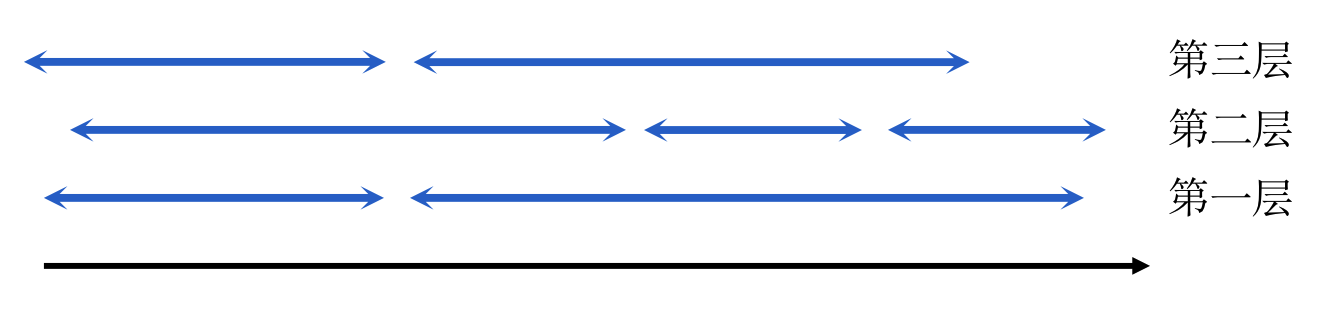
接下来，我们从最简单的情况开始考虑：

只需要一层就可以排列所有区间，使得任意两个区间都不相交，此时意味着所有桌子可以在一次操作（10分钟）之内移动完成

当新增一个区间，使得层数不得不从1变为2时，这意味着新增的区间至少与第一层中的一个区间有交集：

这是因为：如果新增的这一区间与第一层中的所有区间都没有交集，那么它完全可以被合并到第一层，而不会使得层数增长。

在这种思路的启发下，我们可以推论出：假设最终的最优解为N层，对于第N层来说，一定至少存在一个区间，它与前(N-1)层均有交集。

我们使用类似的思路证明：如果对于第N层中的任意一个区间 x，都可以在前 (N-1) 层中找到某一层 i，使得区间 x 与第 i 层没有交集，那么区间 x 一定可以被合并到第 i 层：

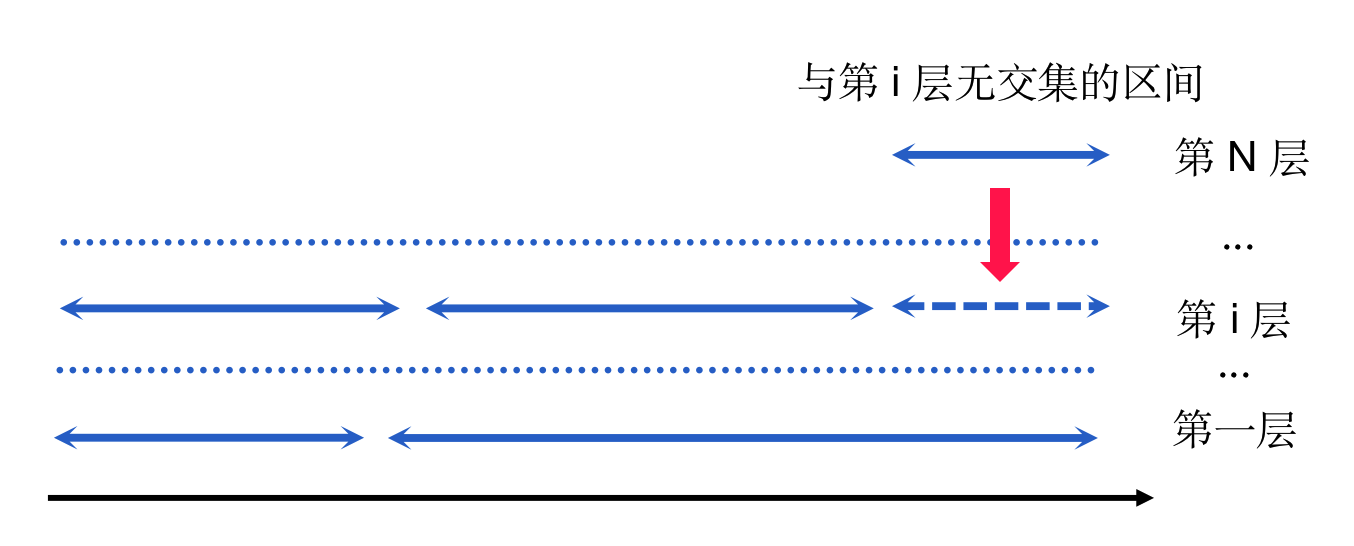
综上，我们只需要统计 x 轴上每个点被区间覆盖的次数，这个次数的最大值就一定等于层数。

题解

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

int h[220] = {};  // 用于记录每个点被覆盖的次数

int main(){
    int T, N, s, e;
    cin>>T;  // T组测试案例
    while (T--){
        cin>>N;  // 要移动的桌子数，即区间总数
        memset(h, 0, sizeof(h));
        for(int i = 0;i < N;i++){
            cin>>s>>e;
            s = (s + s % 2) / 2;  // 将两侧的房间合并到x轴上
            e = (e + e % 2) / 2;
            if(s > e){  // 由于题目并未规定桌子移动的起点小于终点，因此须手动调整
                int t = s;
                s = e;
                e = t;
            }
            for(int j = s;j <= e;j++)
                h[j]++;  // 统计x轴上每个点被覆盖的次数
        }
        int maxVal = 1;
        for(int i = 0;i <= 200;i++){
            maxVal = max(maxVal, h[i]);
        }
        cout<<maxVal * 10<<endl;
    }
    return 0;
}